Факторы, под воздействием которых формируются уровни временного ряда.

В настоящее время уровень  динамического ряда традиционно рассматривается как сумма по крайней мере 4-х составляющих, которые непосредственно не могут быть изменены, соответственно этому целесообразно выделить 4 типа факторов под воздействием которых и формируется уровень yn.

I тип. Долговременные факторы. Формирующие общую с длительной перспективой) тенденцию в изменении анализируемого показателя Yt. Обычно эта  тенденция описывается с помощью той или иной случайной функции Tr(t),  как правило, монотонной. Эту функцию называют функцией тренда (тренд).

II тип. Сезонные. Формирующие периодические повторяющиеся в определенное время года колебания анализируемого показателя. Условимся обозначать не случайной функции S(t). Поскольку эта функция должна быть периодической, в ее аналитическом выражении участвуют тригонометрические функции. Их периодичность обусловлена сущностью задач.

III тип. Циклические. Формирующий такие изменения, как обусловленные действием долговременных циклов экономической, демографической или даже космической периоды. (Волны Кондратьева, демографическое ямы, циклы солнечной активности и т.д.) Они приводят к тому, что значение изучаемого показателя в течение какого-либо времени возрастает, достигает определенного максимума, затем понижается и достигает определенного минимума и вновь возрастает до прежнего значения и т.д. Результат будет обозначен неслучайной функцией C(t).

IV тип. Случайные (нерегулярные). Не поддающиеся учету и регистрации факторы. Их воздействие на формирование значений ряда как раз и обуславливает стахостическую природу элемента y(t), а следовательно и необходимость интерпретации (y(t1), y(t2),…, y(tn)) как наблюдений, произведенных над величинами не являющимися строго детерминированными (определенными). Будем обозначать с помощью случайных величин e(t).

Если динамический ряд разбить на различные компоненты, то он может быть представлен в виде:

Y(t) = Y(Tr(t), S(t), C(t), e(t))                                                    (2.1)

Выбирая ту или иную структурную схему влияния факторов на формирование значений Y(t) мы принимаем некоторую конкретную структурную модель временного ряда. В зависимости от взаимосвязи факторов (I – IV) может быть построена аддитивная или мультипликативная модель ряда динамики. Подчеркнем, что случайная составляющая IV является обязательной для любого ряда, так как случайные отклонения неизбежно сопутствуют любому экономическому процессу.

Если принять аддитивную структурную модель ряда динамики, то в общем случае мы представим соотношение (1)  в виде разложения:

Y(t) = d(1)Tr(t) + d(2)S(t) + d(3)C(t) + e(t),

где   d(i) =

 i = 1, 2,  3

Выводы о том, участвуют или нет факторы данного типа в формировании значений Y(t) могут базироваться как на анализе содержательной сущности задачи, так и на специальном статистическом анализе исследуемого временного ряда.

Аддитивная модель ряда динамики характеризуется главным образом тем, что характер циклических и сезонных колебаний остается постоянным.

Пример 1. Представленные в таблице 2.1. данные – это количество продукции, проданной компанией «Lewplan pic» в течении последних 13 кварталов.

Таблица 2.1

Квартал	Количество проданной продукции, тыс. шт.
Январь – март 2003	239
Апрель – июнь	201
Июль – сентябрь	182
Октябрь – декабрь	297
Январь – март 2004	324
Апрель – июнь	278
Июль – сентябрь	257
Октябрь – декабрь	384
Январь – март 2005	401
Апрель – июнь	360
Июль – сентябрь	335
Октябрь – декабрь	462
Январь – март 2006	481

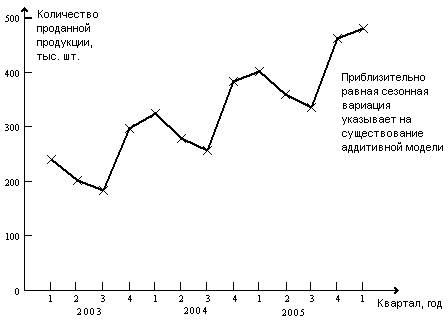Как следует из построенного по этим данным графика (рис. 2.1), возможен возрастающий тренд, содержащий сезонные колебания. Объемы продаж в зимний период (1 и 4 – й квартал) значительно выше, чем в летний (2 – и 3 –й ). Сезонная компонента в течении трех лет практически не меняется. Действительно, хотя в целом объем продаж возрос примерно с 230 тыс. шт. в 2003 г. до 380 тыс. шт. 2005 г., однако, увеличения амплитуды сезонных колебаний не произошло. Этот факт свидетельствует в пользу модели с аддитивной компонентой.

Рис. 2.1.

Если принять мультипликативную структурную модель ряд динамики, то соотношение (2.1) записывается в виде произведения компонент 1, 2, 3:

Y(t) = Tr(t) ×S(t) × C(t) + e(t)

В этой модели характер циклических и сезонных колебаний остается построенным только по отношению к тренду.

Сезонные и циклические колебания присутствуют в значительной части финасово-экономических процессов. Для того чтобы их учитывать при проведении практических расчетов, необходимо уметь их измерять, предвидеть развитие процессов, подверженных сезонности и цикличности.

Решение поставленных задач сводится к выполнению следующих этапов:

- определение наличия во временном ряду тренда и степени его гладкости

- выявления наличия во временном ряду сезонных и циклических колебаний

- фильтрация компонент ряда

- анализ динамики сезонных и циклических колебаний

- исследование факторов, определяющих сезонные и циклические колебания.

- прогнозирование процессов с учетом сезонных и циклических колебаний.