Выявление тренда.

Метод проверки разностей средних уровней. Реализация этого метода состоит из четырех этапов.

На первом этапе исходный временной ряд y1,y2, y3, …, yn разбивается на две примерно равные по числу уровней части: в первой части n1 первых уровней исходного ряда, во второй — n2 остальных уровней (n1 + n2 = n).

На втором этапе для каждой из этих частей вычисляются средние значения и дисперсии:

                                             ; ;

                                           ; .

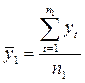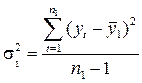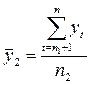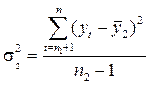Третий  этап заключается в проверке равенства (однородности) дисперсий обеих частей ряда с помощью F-критерия Фишера, которая основана на сравнении расчетного значения этого критерия:

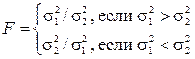
с табличным (критическим) значением критерия Фишера Fa с заданным уровнем значимости (уровнем ошибки) a. В качестве a, чаще всего берут значения 0,1 (10%-ная ошибка), 0,05 (5%-ная ошибка), 0,01 (1%-ная ошибка). Величина (1–a) называется доверительной вероятностью.

Если расчетное значение Fрасч меньше критического Fa, то гипотеза о равенстве дисперсий принимается и переходят к четвертому этапу. Если Fрасч больше или равно Fa, гипотеза о равенстве дисперсий отклоняется и делается вывод, что данный метод для определения наличия тренда ответа не дает. Для получения критического значения воспользуйтесь функцией FРАСПОБР(a; n1; n2).

На четвертом этапе проверяется гипотеза об отсутствии тренда с использованием t-критерия Стыодента. Для этого определяется расчетное значение критерия Стыодента по формуле:

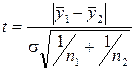                                                   .                                                                   (2.3)

где s — среднеквадратическое отклонение разности средних:

                                           .

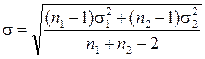Если расчетное значение t меньше критического значения статистики Стьюдента ta с заданным уровнем значимости a, гипотеза принимается, т.е. тренда нет, в противном случае тренд есть. Для получения критического значения воспользуйтесь функцией CTЬЮДРАСПРОБР(a; n1 + n2 -2). Заметим, что данный метод применим только для рядов с монотонной тенденцией.