Если модель оказалась статистически адекватной эмпирическим данным, то предстоит оценить ее качество, значимость и точность.
Проверка качества модели проводится с помощью коэффициента детерминации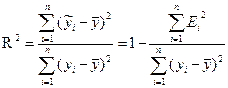 
. Он показывает, какую долю вариации исследуемого признака Y описывает наша модель под воздействием изучаемого фактора. Чем ближе к единице R2, тем лучше качество модели.
Проверка значимости модели проводится с помощью F – теста. Если расчетное значение Fрасч больше критического Fa,n1,n2 при заданном уровне значимости a и со степенями свободы v1=m и v2=n-m (где m – число факторов, включенных в модель), то модель считается значимой.
Для получения критического значения воспользуйтесь функцией FРАСПОБР(a; v1,; v2).
Для оценки точности модели используйте стандартную ошибку оценки прогнозируемого показателя (или среднеквадратическое отклонение от линии тренда)
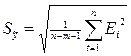, (2.6)
где n-
число опытов, m - число факторов, включенных в модель, и среднюю относительную ошибку аппроксимации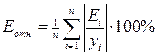 
Если ошибка Еотн не превышает 15%, то точность модели считается приемлемой. В общем случае допустимый уровень точности, а, значит, и надежности прогноза, устанавливает пользователь модели, который в результате содержательного анализа проблемы выясняет, насколько она чувствительна к точности решения и насколько велики потери из-за неточного решения.
Поможем написать любую работу на аналогичную тему