Формирование набора моделей, одна из которых будет использована для получения прогноза, происходит на основе интуитивных приемов (таких, например, как анализ графика ряда динамики), формализованных статистических процедур (исследование приростов уровней), а также содержательного анализа процесса. Предпочтение, как правило, отдается простым моделям, допускающим содержательную интерпретацию. К числу наиболее простых относятся линейные модели роста:
(2.4)
где a0 и a1 параметры модели, а t = 1, 2, …, n.
Рассмотрим оценку параметров модели по методу, сводящемуся к поиску таких значений a0 и a1, при которых сумма квадратов отклонений эмпирических (опытных) данных от рассчитанных по модели (2.4) является наименьшей – метод наименьших квадратов (МНК). Математически критерий такой оценки параметров записывается в виде
Для нахождения минимума функции двух переменных 
следует взять частные производные по a0 и a1, а затем приравнять их к нулю.
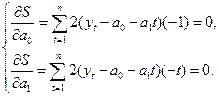
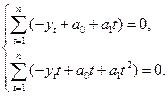
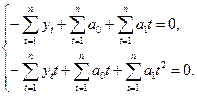
Упрощая, получаем
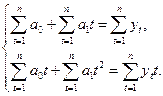
В результате получаем систему нормальных уравнений
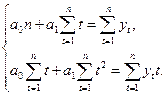
Решая эту систему двух линейных уравнений с двумя неизвестными, получим:
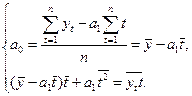
где 
, 
, 
, 
Из второго уравнения получаем: 
,
,
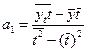
Найдя а1, подставим в первое уравнение и получим 
.
Таким образом, формулы для нахождения параметров а0 и а1:
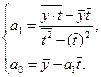(2.5)
Поможем написать любую работу на аналогичную тему