Множественный регрессионный анализ.

Как известно, явления общественной жизни складываются под воздействием не одного, а целого ряда факторов, то есть эти явления многофакторны. Между факторами существуют сложные взаимосвязи, поэтому их влияние комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя. Важным условием является отсутствие между факторами функциональной или сильно корреляционной связи.

Математически задача формулируется следующим образом. Требуется найти аналитическое выражение, наилучшим образом отражающее установленную теоретическим анализом связь независимых признаков с результативным, то есть функцию вида:

yi =f(х1, х2, …, хn) + εi                                 (1)

Данное выражение является классической нормальной моделью множественной регрессии.

Применяя ЭВМ, выбор аппроксимирующей математической функции осуществляется перебором решений, наиболее часто используемых в анализе и решении корреляционно-регрессионных уравнений.

После выбора типа аппроксимирующей функции приступают к многофакторному корреляционному и регрессионному анализу, задачей которого является построение уравнения множественной регрессии и нахождение его неизвестных параметров а0, а1, а2, …, аn.

Параметры уравнения множественной регрессии, как и в случае парной регрессии, находят по способу наименьших квадратов. Затем с помощью корреляционного анализа осуществляют проверку адекватности полученной модели. Адекватную модель экономически интерпретируют.

Частным случаем выражения (1) является уравнение множественной линейной двухфакторной регрессии вида

 ŷх1…хi = a0 + a1·х1 + a2·x2                                  (2)

где ŷх1…хi - расчетные значения зависимой переменной (результативного признака); х1, x2 - независимые переменные (факторные признаки); а0, а1 и а2 – параметры уравнения.

для расчета параметров которой применяется следующая система линейных уравнений:

а0·n + а1·∑х1 + а2·∑х2 = ∑y;

а0·∑х1 + а1·∑х12 + а2·∑x1·х2 = ∑y·x1;                    (3)

а0·∑х2 + а1·∑х1·x2 + а2·∑x22 = ∑y·x2.

В случае линейной трехфакторной связи уравнение регрессии имеет вид:

ŷх1…хi = a0 + a1·х1 + a2·x2 + a3·x3                                (4)

        Для расчета параметров по способу наименьших квадратов используют следуюущую систему нормальных уравнений:

а0·n + а1·∑х1 + а2·∑х2 + а3·∑х3= ∑y;

а0·∑х1 + а1·∑х12 + а2·∑x1·х2 + а3·∑x1·х3 = ∑y·x1;

а0·∑х2 + а1·∑х1·x2 + а2·∑x22 + а3·∑ x2·х3= ∑y·x2.             (5)

а0·∑х3 + а1·∑х1·x3 + а2·∑ x2·х3 + а3·∑ x32= ∑y·x3.

Чтобы получить эту систему, необходимо иметь таблицу значений следующих показателей х1, ·х2, х3, х12, x22, x32, y·x1, y·x2, y·x3, x1·х2, x1·х3, x2·х3

         Для решения уравнения множественной регрессии с n-факторами

ŷх1…хi = a0 + a1·х1 + a2·x2 + …+ an·xn                     (6)

применяется следующая система нормальных уравнений:

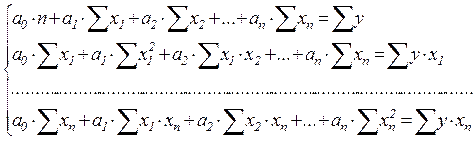         (7)

Вручную целесообразно выполнять построение и анализ только двух-, максимум трехфакторных моделей. Для n>3 все расчеты рекомендуется осуществлять на компьютерах по специальным программам, предусматривающим исчисление параметров уравнения и показателей, используемых для проверки его адекватности.