Модели бинарного выбора

Модели бинарного выбора широко используются в экономических и социальных исследованиях, особенно в экономике труда, при проведении анализа на микро-уровне. Покажем их специфические свойства на примере модели трудовой активности населения, исходные предпосылки которой состоят в следующем. Индивидуум в определенный период времени может работать или искать работу (y=1) или не делать этого (y=0). Предположим, что состояние “работать” или “не работать” определяется набором факторов (возраст, семейное положение, образование, опыт работы и т. д.), и соответствующие вероятности можно представить в следующем виде:

P(y=1)= F(a¢x);

P(y=0)=1–F(a¢x).                          (10.41)

Вектор коэффициентов  a отражает влияние факторов, например, характеризующих положение индивидуума в обществе, на рассматриваемую вероятность.

Одной из основных проблем при построении моделей бинарного выбора является обоснование функционала F(a¢x). Например, предположим, как и в случае “классических” эконометрических моделей, что вероятности соответствующих событий могут быть представлены в виде линейной функции от значений рассматриваемых факторов:

 

F(a¢x)=a¢x=a0+a1x1+...+anxn,                (10.42)

где a0, a1,..., an – параметры модели; x1,..., xn – значения независимых факторов.

Тогда, приняв M=F(a¢xt), соответствующую эконометрическую модель можно представить в следующем виде:

yt =M+(yt –M)=a¢x t +e t.                  (10.43)

где M= – условное математическое ожидание переменной yt   при условии, что вектор независимых переменных равен x t.

Линейная форма модели представляет определенное удобство для раскрытия содержания, входящих в  нее слагаемых. Прежде всего заметим, что между их значениями выполняется следующие соотношения (см. табл. 10.1).

 

Таблица 10.1

уt Внимание! Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы. Расчет стоимостиГарантииОтзывы	P(уt=...)=	et
1	a¢xt	1–a¢xt    (с вероятностью a¢xt)
0	a¢xt	–a¢xt   (с вероятностью 1–a¢xt)

Из табл. 10.1. следует, что ошибки et  модели (10.43) имеют следующие характеристики:

M=a¢xt(1–a¢xt)+ (1–a¢xt)( –a¢xt)=0;

D=a¢xt(1–a¢xt)2+(1–a¢xt)(–a¢xt) 2=a¢xt(1–a¢xt)(1–a¢xt+a¢xt)=

=a¢xt(1–a¢xt).                          (10.44)

где D – условная дисперсия ошибки et   при условии, что вектор независимых переменных равен x t.

 Рассмотрим в качестве критерия выбора оценок параметров модели (10.43) минимум суммы дисперсий ее ошибок et:

a¢xt)2+a¢xt) 2=xt(1–a¢xt)2+1–a¢xt)(–a¢xt)2=

=xt(1–a¢xt)= min.                (10.45)

Используя МНК для оценки параметров модели (10.43) при критерии (10.45), получим следующую систему “нормальных” уравнений, относительно неизвестных оценок а0, а1,..., аn:

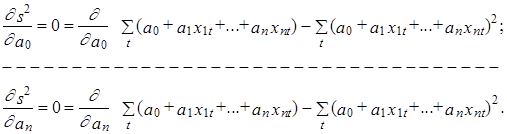
Выполнив дифференцирование с учетом попарной независимости коэффициентов между собой и со значениями факторов хit, i=1,2,...,T, эту систему можно представить в следующем виде:

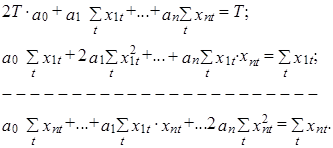
В свою очередь, последняя система может быть представлена в векторно-матричном виде следующим образом:

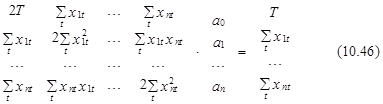
или в компактной форме записи как

X×a=z,                             (10.47)

где матрица 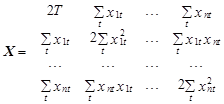   и  вектор-столбец .

Из выражения (10.47) непосредственно вытекает, что неизвестные оценки параметров бинарной модели линейного типа могут быть получены на основании следующего выражения:

a=X–1×z,                             (10.47)

Однако линейная интерпретация (10.42) закона распределения вероятностей  достаточно “неудобна” по своим “эконометрическим следствиям”.

Во-первых, заметим, что из выражения (10.44) вытекает, что ошибка e  гетероскедастична, поскольку дисперсия ошибки зависит от вектора x.  В таких условиях оценки параметров a модели (10.43), полученные на основе выражения (10.48), являются неэффективными. Для получения эффективных оценок ее параметров, необходимо использовать обобщенный МНК.

Во-вторых, любой метод оценки параметров линейных моделей бинарного выбора не дает гарантий, что результат произведения a¢x  может принимать значения только на интервале . С учетом выражения (10.44) несложно заметить, что при отрицательных значениях этого произведениях и значениях больших единицы будет иметь место и другой абсурдный результат – отрицательная дисперсия остатков. Это обстоятельство существенно ограничивает область применения линейной модели бинарного выбора. На практике она используется только для предварительной обработки данных и для сопоставления с результатами, полученными более тонкими методами.

Из приведенных рассуждений вытекает, что модель бинарного выбора должна удовлетворять двум условиям:

и

где a¢x®+¥ – область значений x, при которых P(y=1)=1, а a¢x®–¥ – область значений x, при которых P(y=1)=0.

При этом между значениями составных частей регрессионного уравнения должно выполняться следующее соответствие (см. табл. 10.2).

 

Таблица 10.2

уt	P(уt=...)=	et
1	F(a¢xt)	1– F(a¢xt)
0	1– F(a¢xt)	–(1– F(a¢xt))

Условиям (10.49) отвечает, например, функция F(a¢x), близкая к закону нормального распределения, график которой представлен на рис. 10.2. Ее использование позволяет снять рассмотренные выше ограничения моделей бинарного выбора. Модели с функционалом, обладающим свойством “нормального закона“,  в литературе получили название  probit-моделей:

P(Y=1)=ò (a¢x).                    (10.50)

где Ф(.) – функция стандартного нормального распределения, зависящая от значений факторов x и параметров a, j(u)– функция плотности распределения стандартной нормальной переменной u.

В предположении о независимости и гомоскедастичности ошибок et   функцию j(u) можем записать в следующем виде:

j(a¢xt)=

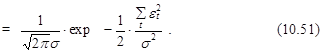
Заметим, что s2 в выражении (10.51) является неизвестным параметром, который должен быть оценен, как и вектор параметров a.

 

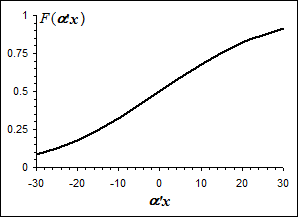
Рис.10.2   График функции закона распределения, близкого к нормальному.

Из выражения (10.51) вытекает, что между значениями независимой переменной уt  и j(a¢xt) выполняется следующее соотношение (см. табл. 10.3).

Таблица 10.3

уt	j(a¢xt)
1
0

Не менее широко в моделях бинарного выбора используется и логистическое распределение:

P(Y=1)=L(a¢x).                     (10.52)

где L(.) представляет собой  интегральную функцию логистического распределения.

Модели, построенные на его основе, называются logit-моделями. Несложно заметить, что в данном случае между составными частями регрессионного уравнения выполняется следующее соотношение (см. табл. 10.4).

Таблица 10.4

уt	P(уt=...)=	et
1
0

Вопрос о том, какое из вышеназванных распределений более подходит для практических исследований, остается открытым. На участке a¢xÎ оба они ведут себя практически одинаково. Однако вне этого участка, т. е. на хвостах распределения, значения функционалов Ф(a¢x) и L(a¢x) имеют некоторые отличия. В частности, логистическое распределение имеет более “тяжелый хвост”, чем нормальное. Практика показывает, что при отсутствии существенного преобладания одной альтернативы над другой, а также для выборок с небольшим разбросом переменных, выводы, полученные на основе probit- и logit-моделей, как правило, совпадают.

В общем случае из выражения (10.41) для модели бинарного выбора вытекает, что условное математическое ожидание зависимой переменной при заданном наборе факторов может быть определено следующим выражением:

M=0×+1×F(a¢xt)=F(a¢xt).            (10.53)

Одно из направлений использования результата (10.53) в анализе рассматриваемых явлений связано с оценками так называемого маржинального эффекта факторов, входящих в модель. Маржинальный эффект фактора xit, i=1,2,...,n; t=1,2,..,T показывает  изменение функции F(a¢xt) (характеризующей вероятность того, что у=1) при изменении фактора xit   на единицу.

Маржинальные эффекты факторов xt  для модели бинарного выбора оцениваются на основе следующего  выражения:

¶M/¶xt={¶ F(a¢xt)/ ¶(a¢xt)}×a=f(a¢xt)×a,            (10.54)

где f(.) – плотность безусловного распределения, соответствующая интегральному распределению F(.) и дифференцирование осуществляется по вектору xt. В частности, для нормального распределения маржинальный эффект рассчитывается  по формуле

¶M/¶xt=f(a¢xt)×a,                        (10.55)

где f(.) – плотность стандартного нормального распределения.

Для логистического распределения производная функции этого закона по факторам xt  функция f(a¢xt) имеет следующий вид:

¶L/¶xt=ea¢x /(1+ ea¢x)2 =L(a¢xt)×.   (10.56)

Соответственно в logit-модели маржинальные эффекты определяются как

¶M/¶xt=L(a¢xt)××a,              (10.57)

Из выражений (10.54)–(10.57) вытекает, что величина маржинального эффекта для probit- и logit-моделей зависит от значений независимых факторов x. В связи с этим полезно будет определить так называемый “средний маржинальный эффект” в области существования значений независимых факторов.

На практике возможны два подхода к его оценке. Первый основан на усреднении значений независимых факторов, т. е. сначала рассчитываются выборочные средние всех факторов , i=1,2,..., п, а затем для оценки среднего эффекта определяется f(a¢)×a. В соответствии со вторым подходом маржинальные эффекты оцениваются для каждого наблюдения, затем по полученным оценкам этих индивидуальных маржинальных эффектов определяется его среднее значение.

 Поскольку функция (10.51) у рассматриваемых моделей непрерывна, то в соответствии с теоремой Слуцкого* на больших выборках оба подхода будут давать один и тот же набор средних маржинальных эффектов. Но это неверно для малых выборок. Практика показывает, что в этом случае лучшие результаты дает второй подход, основанный на усреднение индивидуальных маржинальных эффектов.

Заметим, что средний маржинальный эффект бинарной независимой переменной (например, с) можно определить как следующую разность: P–P, где  – вектор выборочных средних значений остальных независимых переменных х.

Обратим внимание на то, что результаты моделей бинарного выбора могут иметь разнообразное содержание. В частности, их можно проинтерпретировать в терминах выгоды или ущерба. Рассмотрим такую интерпретацию на примере модели крупной покупки. Исходными данными (наблюдаемыми переменными) в этом случае являются сведения о покупке (1 – покупка сделана, 0 – в противном случае) и факторы, характеризующие субъекта, потребителя (доход, пол, возраст и т. д.). Далее предполагается, что покупка имеет место, если она приносит выгоду потребителю, и покупка отсутствует, если такой выгоды нет, и даже возможен “ущерб” (например, покупка бесполезна).

Ненаблюдаемую (латентную) выгоду, получаемую t-м потребителем от покупки, будем моделировать как переменную yt*, определяемую следующим выражением:

yt*=a¢xt+et,                                   (10.58)

где a¢xt  в данном случае называется индексной функцией (index funktion);   et – ошибка модели, в отношении которой делается предположение, что она имеет стандартное нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.

Вероятность получения t-м потребителем выгоды от покупки может быть определена следующим образом:

P(yt*>0)=P(a¢xt+et>0)=P(et>–a¢xt).              (10.59)

Если распределение симметрично (каковыми являются нормальное и логистическое), то выражение (10.59), можно представить в следующем виде:

P(yt*>0)=P(e<a¢xt)=F(a¢xt).                      (10.60)

В качестве примера модели типа (10.58)–(10.60) рассмотрим модель миграции, разработанную Нейкостином и Циммером (Nakosteen, Zimmer, 1980). В ее основе лежит предположение о том, что индивидуум принимает решение о переезде, если это приносит ему определенную выгоду, которая оценивается на основе сопоставления доходов в настоящем и “новом” месте его проживания, затрат на переезд.

Доход yp*, который индивидуум может получить в данной местности настоящего проживания за год, определяется как

yp*=a¢xp+ep,                             (10.61)

где a – вектор значений параметров; xp – вектор  независимых переменных, характеризующих индивидуума, например, возраст, образование, опыт работы, и т. д.; ep – ошибка модели.

Если индивидуум переезжает на новое место, то его доход ym*   будет определяться согласно следующему выражению:

ym*= b¢xm+em,                              (10.62)

где b – вектор значений параметров; xm – вектор  независимых переменных, состав которых может как совпадать, так и не совпадать с составом компонент вектора xp (включать, например, возможность получения более престижной должности); em – ошибка модели.

Переезд связан с определенными затратами C*, которые могут быть связаны линейной зависимостью со статусом индивидуума (предприниматель, наемный работник, семейный или несемейный и т. д.):

C*= g¢z+u,                             (10.63)

где z – вектор  независимых переменных, характеризующих статус индивидуума; u  – ошибка модели.

С учетом вышеперечисленного выгода от переезда может быть представлена в следующем виде:

N*=ym*– yp*– C*=b¢xm –a¢xp –g¢z+(em –ep– u)=d¢w+e,   (10.64)

где w – вектор  независимых переменных, характеризующих индивидуума, условия его жизнедеятельности в местах его жительства и т. п., которые влияют на уровень доходов и затраты на переезд; e=em –ep– u – ошибка модели.

В целом, вероятность переезда P(N=1) определяется следующим образом:

P(N*>0)=P(d¢w+e>0)=P(e>–d¢w).             (10.65)

Выражение (10.65) полностью соответствует выражению (10.59).

Альтернативную интерпретацию данных об индивидуальных предпочтениях дает модель случайной полезности (random utility model). Согласно этой интерпретации латентные (ненаблюдаемые) переменные предыдущей задачи, т. е. ym   и yp, представляют собой полезности для индивидуума двух выборов (переезжать или не переезжать). В другом примере латентные переменные могут характеризовать полезность аренды дома и полезность владения домом. Статистика индивидуальных выборов, т. е. значения yt=1 и yt=0, дают возможность оценить, какая из альтернатив имеет большую полезность при соответствующих наборах факторов, но при этом величина полезности остается неопределенной. Обозначим полезность аренды дома через Ua, а полезность владения домом – через Ub. Наблюдаемый индикатор yt  равняется 1, если     Ua>Ub, и равняется 0, если Ua £Ub.

Общая постановка модели случайной полезности выглядит следующим образом:

Ua=a¢a x+ea;

Ub=a¢b x+eb.                              (10.63)

где aa  и ab – различающиеся между собой вектора параметров модели; индексы а и b характеризуют варианты выбора.

Тогда, вероятность выбора варианта а (наблюдаемая переменная  y принимает значение 1) определяется по следующей формуле:

P(y=1|x)=P=P=

= P= P.       (10.64)

На практике по известным значениям наблюдаемой переменной yt  оценивается вектор a=aa –ab.

Рассмотренные выше модели использовали, так называемые индивидуальные данные. Каждое наблюдение содержало набор значений , характеризующих реальный выбор отдельного индивидуума и соответствующий вектор независимых факторов. Вместе с тем, часто при построении моделей бинарного выбора используются групповые данные, которые выражают результаты подсчетов или пропорций. Обозначим через kt  количество индивидуумов, имеющих одинаковые значения, характеризующих их признаков (т. е. одинаковый вектор xt). Индекс t в этом случае выражает различные вектора признаков xt  и соответствующие количества индивидуумов kt, обладающих ими. Пусть наблюдаемая зависимая переменная Nt   выражает долю индивидуумов, у  которых yt=1, в общем числе индивидуумов kt. С учетом этого информация для фиксированного индекса t выглядит как , t=1,..., T. Для сгруппированных таким образом данных представим  зависимость доли Nt  от факторов-признаков, характеризующих индивидуумов t-й группы,  в следующем виде:

Nt=F(a¢xt)+et =pt +et,

M=0;   

D=pt ×(1–pt)/kt.                          (10.68)

где в качестве функции F(a¢xt) обычно используются функции законов нормального и логистического распределений; pt  – оценка доли Nt; et  – ошибка модели.

В заключение раздела, посвященного рассмотрению моделей бинарного выбора, объясним происхождение терминов logit и probit. Из выражения (10.68) следует, что дисперсия ошибки e  гетероскедастична. Поскольку функция F(a¢xt) предполагается нелинейной, то для оценки параметров следовало бы применить нелинейный МНК с весами, однако можно предложить менее громоздкий подход к решению данной задачи. Для этого обозначим через F(Nt) значение интегральной функции закона распределения в точке Nt. Тогда можно показать, что обратное значение этой функции F–1(Nt) допускает следующее представление*:

F–1(Nt)»a¢xt +et/f(pt)

или

F–1(Nt)=zt »a¢xt +ut,                           (10.66)

где f(pt)– значение функции плотности, соответствующей интегральной функции закона распределения F(.), в точке pt: ut=et/f(pt) – ошибка, обладающая следующими характеристиками:

M=0;

 

Если F(a¢xt) является  логистической функцией, т. е.

pt =exp(a¢xt)/,

то несложно показать, что

 

F–1(pt )=ln=a¢xt.                   (10.71)

Функция типа (10.71) в научной литературе получила название logit-pt. В связи с этим модели бинарного выбора, в основе которых лежит логистическое распределение, обычно называют logit-модели.

Для нормального распределения обратная функция Ф–1(pt) называется нормитом-pt. Функция Ф–1(pt) может принимать отрицательные значения, обычно не превышающие –5. Чтобы избежать работы с отрицательными числами к значению функции на практике добавляется число 5. Функция (нормит-pt +5) получила название probit-pt. Поэтому модели бинарного выбора, основанные на нормальном распределении, называются probit-модели.

Двумерные и многомерные probit-модели.

Probit-модели могут быть могут быть использованы для определения вероятностей сложных событий, выражаемых в виде комбинаций некоторых наборов простых событий, каждое из которых имеет два альтернативных варианта, например, переезд (непереезд) на новое место жительства и аренда (покупка) жилья и т. п. В этом случае данные вероятности могут быть определены как вероятности выбора в рамках многомерных альтернативных вариантов.

 Для каждого индивидуума t (t=1,2,...,Т) модель, определяющая вероятности двух событий, может быть представлена в виде следующей системы:

y1t*=a¢1x1t +e1t, если y1t=1, то y1*>0, если y1=0, то y1*£0;

y2t*=a¢2x2 t +e2t, если y2t=1, то y2*>0, если y2=0, то y2*£0.   (10.72)

Латентные переменные y1t * и y2t *  модели (10.72) могут интерпретироваться в терминах выгоды, получаемой в зависимости от принятого решения соответственно в первом и во втором случаях; х1t и х2t   – векторы значений независимых факторов, соответствующих сделанному выбору; e1t  и e2t – ошибки соответственно первого и второго уравнений; r  – коэффициент ковариации ошибок e1  и e2.

Закон совместного распределения ошибок модели e1  и e2 в общем случае характеризуется следующими параметрами:

 

M=M=0;

D=D=1* ;

Cov=r,

Согласно модели (10.72) возможны следующие комбинации решений:

Наблюдаемые комбинации образуют массив зависимых переменных модели (10.72).

В системе (10.72) допускается, что события являются зависимыми между собой, что означает существование ненулевой ковариационной связи между ошибками e1  и e2. Например, возможность приобретения жилья на новом месте может способствовать принятию решения о переезде или, наоборот, переезд обусловливает необходимость аренды жилья.

 Для определения функции закона распределения введем следующие обозначения: q1t=2y1t–1 и q2t=2y2t–1*. Тогда qjt=1, если уjt=1, и qjt=–1, если уjt=0, для j=1,2. Введем также в рассмотрение следующие переменные:

zjt=a¢jxjt     и wjt= qjt×zjt, j=1,2

и

rt*=q1t× q2t×r.

Вероятность того, что зависимые переменные Y1  и Y2 системы (10.72) для конкретного индивидуума принимают соответственно значения y1t  и  y2t, при, например, нормальном виде закона их совместного распределения рассчитывается как

P(Y1=y1t, Y2=y2t)=F2(w1t, w2t, rt*),                    (10.74)

где F2(.) – функция нормального закона совместного  распределения случайных переменных Y1  и Y2, имеющая следующий вид:

F2(w1t, w2t, rt*)=ò ò

где u1  и u2 – переменные интегрирования и плотность этого распределения имеет следующий вид:

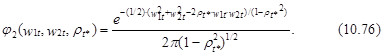
Для определения маржинальных эффектов в модели (10.72) введем в рассмотрение вектор хt, являющийся объединением векторов х1t  и х2t* , и вектор коэффициентов g1, такие что a1¢х1t=g1¢хt. Вектор g1  составлен из элементов вектора коэффициентов a1  и нулей, стоящих на позициях, которые соответствуют переменным второго уравнения. Аналогичным образом введем вектор коэффициентов g2: a2¢х2t=g2¢хt. Тогда вероятность того, что значения y1  и y2 одновременно будут равны единице определяется следующим выражением:

P(y1=1, y2=1)=F2.                 (10.77).

Маржинальные эффекты независимых факторов xt для P(y1=1, y2=1) могут быть определены согласно следующему выражению:

g1t×g1+g2t×g2,

где

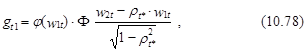
Для получения gt2  индексы 1 и 2 в выражении (10.78) нужно поменять местами* .

Математические ожидания зависимых переменных yj, j=1,2  для конкретных наборов независимых переменных хt в соответствии с выражением (10.50) определяются как

M= F(gj¢×xt), j=1,2.                (10.79)

Для модели (10.72) можно также определить условные математические ожидания переменных y1t  и y2t.

Например, математическое ожидание зависимой переменной первого уравнения при условии, что y2=1, определяется согласно формуле условной вероятности следующим образом:

M=P=

=P/P=

=F2(g1¢×xt, g2¢×xt, r t*)/F(g2¢×xt)                  (10.80)

Аналогично определяется математическое ожидание зависимой переменной второго уравнения при условии, что y1=1.

Маржинальные эффекты факторов xt  для функции типа (10.80) рассчитываются как

¶M/¶xt=

=×.     (10.81)

Аналогичным образом могут быть построены модели с тремя и более зависимыми переменными, с учетом того, что функционал F должен выражать их совместное распределение.

Многомерные модели бинарного выбора с цензурированием.

Бывают ситуации, когда наблюдаемые переменные в двумерной probit-модели цензурируют одна другую. Например, при оценке возможности кредитования Бойз (Boyes et al., 1989) анализировал данные по следующему правилу:

y1=1, если индивидуум t не получает кредит, y1=0 в противном случае;

y2=1, если индивидуум t просит кредит, y1=0 в противном случае.

Для конкретного индивидуума переменная  y1    не наблюдаема, пока y2 не принимает значение 1. Таким образом, возможны следующие наборы значений зависимых переменных:

(Сравните с (10.73)).

Вероятности событий, определенных выражениями (10.82), согласно (10.75) оцениваются следующим образом:

P(y2=0)=1–F(a2¢×x2);

P(y1=0, y2=1)=F 2(–a1¢×x2, a2¢×x2, –r);

P(y1=1, y2=1)=F 2(a1¢×x2, a2¢×x2, r),            (10.83)

где Ф(.) – функция закона нормального распределения, а функция F 2(.) определена выражением (10.75).