Эконометрические модели с ошибками в переменных

В общем случае следует разделять три ситуации, связанные с ошибками переменных эконометрической модели: ошибки имеют место у зависимой переменной, у независимых переменных и у тех и других вместе взятых. Рассмотрим возможные последствия этих ошибок с точки зрения проблемы получения “качественных” оценок параметров модели.

1.   Ошибки измерения зависимой переменной у.

Представим нелинейную эконометрическую модель в векторно-матричной форме записи

y=X×a+e,

где, как и ранее, X  – матрица значений независимых факторов размера Т´(п+1), a – вектор коэффициентов модели, состоящий из п+1 компоненты, а e – вектор ошибки модели, обладающий “классическими” свойствами, Сov(e)=s2×E, ошибки и факторы независимы.

В отношении вектора у будем предполагать, что его компоненты, являющиеся истинными значениями переменной у в моменты t=1,2,...,Т; измерены с ошибкой ut и данные измерений представлены в виде следующих сумм:

где  – измеренное значение зависимой переменной в момент t, а  ut – ошибка, допущенная при измерении этого значения. Соответственно  характеризует вектор измеренных значений зависимой переменной, а и –  вектор их ошибок.

С учетом (10.1) эконометрическую модель можно представить в следующем виде:

=X×a+(e+и).                              (10.2)

Дальнейшие выводы зависят от свойств ошибки и. Логично предположить, что вектор и и столбцы матрицы X (значения факторов модели) независимы, и что математическое ожидание ошибки и равно нулю: M=0, и в ряду ut   отсутствует автокорреляция. В этом случае очевидно, что привнесение ошибки измерения зависимой переменной ведет лишь к увеличению дисперсии модели, поскольку она при независимости ошибок et и ut определяется следующим выражением:

s2=se2+su2.                                (10.3)

Наличие у ошибки ut каких-либо свойств, отличающих ее от “белого шума” или характеризующихся ее статистическими взаимосвязями со значениями параметров хit, приводит к тому, что аналогичные свойства появляются и у суммарной ошибки модели (10.2). В этом случае при оценке ее параметров необходимо использовать соответствующие методы (обобщенный МНК, метод инструментальных переменных).

Если математическое ожидание ошибки и отлично от нуля (случай систематической ошибки измерений), то очевидно, что использование, например, МНК при оценке параметров модели (10.2) приведет к смещенным оценкам, поскольку в этом случае  математическое ожидание вектора ошибок оценок параметров (Х¢×Х)–1×Х¢(e+и) будет отлично от нуля, так как M¹0 в силу M¹0. Однако, если величина смещения ошибки и  известна, то корректировкой исходных данных зависимой переменной уt на ее величину несложно перейти к исходным условиям задачи, когда , где   – скорректированная ошибка зависимой переменной.

2.   Ошибки измерения независимых переменных хi, i=1,2,..., n.

Предположим, что истинные значения независимых переменных равны хit, а их измеренные значения равны , и связь между ними определена следующим выражением:

где vit – случайная ошибка измерения i-й переменной в момент  t, i=1,2,..., n; t=1,2,..., T.

В отношении этой ошибки будем предполагать, что ее математическое ожидание равно нулю, дисперсия (постоянная по времени) равна  для каждого i во временном ряду ошибки vit отсутствуют автокорреляционные связи и ошибки измерения различных параметров независимы между собой, т. е. cov(vi, vj)=0.

Соответствующие матрицы значений независимых переменных в этом случае связаны следующим образом:

где  и Х – матрицы измеренных и истинных значений независимых переменных соответственно, а V – матрица ошибок измерения.

В этом случае при использовании данных измерений независимых переменных эконометрическая модель может быть представлена в следующем виде:

у=×a+(e–V×a),                             (10.6)

гдеe–V×a  представляет собой вектор ошибки такой модели.

Оценивая коэффициенты модели (10.6) с помощью МНК, получим

a+(e–V×a)]=

=a+(e–V×a),                           (10.7)

где  – вектор оценок коэффициентов модели a.

Из выражения (10.7) непосредственно следует, что свойства оценок   определяются вторым слагаемым его правой части. При этом несложно убедиться, что, в частности, оценки   являются асимптотически смещенными (а значит и смещенными при конечном объеме выборки Т) и несостоятельными.

Заметим, что при ограниченной выборке, т. е. значение Т конечно, математическое ожидание разности векторов параметров модели и их оценок определяется следующим выражением:

M=M=M–

–M.                     (10.8)

Даже при условии независимости истинных значений факторов хit и ошибки et, второе слагаемое правой части этого выражения отлично от нуля. Чтобы показать это, выразим одну из  матриц  из (10.8), с учетом ее вида (10.5). С учетом независимости х и e, х и V и нулевых математических ожиданий ошибок e и V, получим

M=M=

M¹0,                          (10.9)

поскольку математическое ожидание произведения матриц V¢V не равно нулю.

В частности, при отмеченных выше свойствах ошибки V несложно показать, что

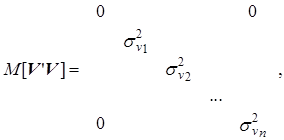
где дисперсия ошибки измерения i-го фактора может быть определена следующим выражением

а нулевой элемент на главной диагонали характеризует нулевую дисперсию единичного столбца матрицы .

Для модели с центрированными переменными в случае одной независимой переменной несложно показать, что величина смещения определяется следующим выражением:

Cov=M=–a1× M= –a1×sv2.

(10.11)

где , – вектора центрированных измеренных и истинных значений независимой переменной соответственно; v – вектор ошибки измерения независимой переменной; sv2 – дисперсия этой ошибки, a1 – параметр модели, которая в данном случае имеет следующий вид:

=a1×+et.

Наличие или отсутствие свойства состоятельности у оценок  (в предположении, что существует предел по вероятности вторых моментов измеренных значений переменных , т. е. plim¹0 и предел по вероятности вторых моментов ошибки измерений plim¹0) зависит от равенства (или неравенства) нулю предела plim, где, напомним,  обозначение plim характеризует предел по вероятности при Т®¥ (см. раздел 1.5). Несложно заметить, что это выражение преобразуется к следующему виду:

plim= plim(1/T××e)–plim(1/T××V)×a.

При предположении об асимптотической независимости (т. е. при Т®¥) ошибки e, измеренных значений факторов и ошибок их измерения получим

plim(1/T××V)=plim(1/T×Х¢×V)+ plim(1/T× V¢×V)= plim(1/T× V¢×V).

Откуда следует, что асимптотическое смещение оценок параметров эконометрической модели с ошибками измерений независимых переменных определяется следующей формулой:

plim=–plim (1/T×)–1× plim(1/T× V¢×V)×a.     (10.10)

Очевидно, что правая часть этого выражения не равна нулю, поскольку пределы plim (1/T×)–1 и plim(1/T× V¢×V) по определению существуют и второй из них представляет собой асимптотическую ковариационную матрицу ошибок измерений.

Поскольку оценка  смещенная для конечных значений Т и несостоятельная, то очевидно, что она и асимптотически смещенная.

3.   Ошибки измерения зависимой переменной у и независимых переменных, хi, i=1,2,..., n.

Несложно заметить, что при наличии ошибок измерения у зависимой и независимых переменных эконометрическая модель может быть представлена в следующем виде:

a+(e+u–V×a),                             (10.12)

где e – вектор ошибки истинной модели; u – вектор ошибки измерений зависимой переменной, V – матрица ошибок измерений независимых переменных.

Даже при вполне естественных предположениях о взаимной независимости ошибок e, u  и V, истинных значений переменных хi  и этих ошибок, используя примененные в двух других случаях подходы,  можно показать, что:

а)   дисперсия такой модели увеличивается по сравнению с моделью, исходные данные которой измерены без ошибок;

б)  использование обычного МНК дает смещенные оценки ее параметров.

В частности, заметим, что дисперсия модели (10.12) при этих предположениях определяется следующим выражением:

s2=M=M,                        (10.16)

При оговоренных свойствах инструментальных переменных несложно увидеть, что математическое ожидание ошибки  равно нулю, т. е. M=0, а ковариационная матрица ошибок определяется выражением:

Cov()=M=

(e–V×a)×(e¢–a¢×V¢)×            (10.17)

В условиях независимости ошибок e и V выражение (10.17) приобретает следующий вид:

Cov()=(× (10.18)

где M(V×a×a¢×V¢) является ковариационной матрицей вектора V×a, т. е. M(V×a×a¢×V¢)=Сov(V×a).

При условии отсутствия корреляционных связей у ошибок et и vit и независимости ошибок измерения vit, vjt, i¹j несложно увидеть, что выражение (10.18) приобретает следующий вид:

Cov(e)+M(V×a×a¢×V¢)=se2×Е+sv2×Е=(se2 +sv2)×Е,        (10.19)

где sv2 – взвешенная по параметрам a  дисперсия независимых переменных, определяемая в условиях независимости ошибок vit и vjt  следующим выражением:

В этом случае ковариационная матрица оценок параметров  модели (10.15) будет иметь следующий вид:

Cov()=(se2+sv2)× (

На практике при известных оценках параметров  сомножитель se2+sv2=s2  может быть определен на основе следующего выражения:

Асимптотическая несмещенность и состоятельность оценок , полученных с использованием инструментальных переменных z на основании выражения (10.14), вытекает из предполагаемой их независимости в пределе при Т®¥ с ошибками e и V, и конечных перекрестных предельных моментов с измеренными значениями переменных хi, т. е. , а также независимости и отсутствии автокорреляции у ошибок e и V. Иными словами, матрица Z и ошибки e и V должны обладать следующими предельными свойствами:

plim(1/T×e×e¢)=se2;

 plim(1/T× V¢×V)=sv2;

plim(1/T×e¢×a×V)=0;

plim(1/T× Z¢×e)=0;

plim(1/T× Z¢×V×a)=0;                                   (10.23)

plim(1/T× Z¢×)=;

plim(1/T× Z¢× Z)=.

С учетом (10.23) для выражения (10.16) несложно показать, что plim=plim=0, а ковариационная матрица оценок  в пределе определяется следующим выражением:

(e–V×a)×(e¢–a¢×V¢)×(10.24)

Учитывая, что

 (e–V×a)×(e¢–a¢×V¢)×Z)=

получим следующее выражение для асимптотической матрицы автокорреляций ошибок вектора :

которое на практике заменяется выражением (10.21).

В разделе  3.3  было отмечено, что основным недостатком использования инструментальных переменных при оценке параметров эконометрических моделей, является увеличение дисперсий этих оценок. При этом их дисперсии увеличиваются пропорционально снижению силы статистической взаимосвязи факторов хi  и соответствующих инструментальных переменных zi. При высокой корреляции между этими переменными снижение эффективности не столь значительно.

Напомним, что увеличение дисперсии оценок при слабой коррелированности переменных zi и , как и ранее, объясняется уменьшением диагональных элементов матриц (Z¢X) и (X¢Z), а, следовательно, и ростом соответствующих показателей их обратных матриц, что ведет к росту диагональных элементов в матрице Cov() (см. выражение (10.21)).

Таким образом, при выборе инструментальных переменных должно соблюдаться следующее правило: переменные zi  должны коррелировать с измеренными значениями факторов , но быть статистически не связанными с ошибками их измерения vi.

Ранее в разделе       было показано, что такими свойствами обладают “сглаженные” значения переменных , т. е. , определенные на основе аппроксимирующих функций =j(wi, t), =j(t), где wi – набор новых переменных, определяющих тенденции развития фактора хi, а t – фактор времени.

В отсутствии таких “сглаженных переменных”, удовлетворительные результаты можно получить, используя в качестве инструментальных значений переменных zi  ранги соответствующих переменных , т. е. числа типа 1,2,3,..., характеризующие порядковые номера уровней этих переменных в их ранжированном ряду. Иными словами, 1 присваивается значению zi t, если переменная  принимает наименьшее значение в ряду переменных  при t=1,2,....,Т; значение zik=2, если значение  является наименьшим среди всех оставшихся значений переменных и т. д.