Различные классы моделей финансовой эконометрики базируются на тех или иных предположениях относительно корреляционных взаимосвязей, характерных для наблюдаемого временного ряда определенного финансового показателя, в качестве которого могут выступать непосредственно цены, доходы (чистые, валовые, логарифмические), а также их приросты, ошибки моделей и некоторые другие характеристики. Примером этих характеристик могут являться также и функциональные преобразования финансовых показателей, например, линейные и степенные функции от них.
Значительная часть таких взаимосвязей может быть определена общим выражением, означающим отсутствие автоковариационных связей между временными рядами, образованными различными функциональными преобразованиями рассматриваемого финансового показателя, следующего вида:
Cov(f(zt), g(zt–k))=0, k=1, 2,... (7.15)
В выражении (7.15) в качестве аргумента z функций f и g выступает одна из перечисленных выше характеристик финансового показателя (цена, какая-либо из ее производных, функция от цены или ее производной и т. п.), рассматриваемая в моменты t и t–k соответственно.
Выражение (7.15) часто называют ортогональным условием. Различные сочетания входящих в него функций соответствуют вполне определенным предпосылкам относительно характера взаимосвязей во временном ряду финансового показателя (исходные гипотезы), которые и кладутся в основу описывающей этот ряд модели. Рассмотрим некоторые из наиболее известных предпосылок более подробно.
Одна из самых “старых” гипотез относительно взаимосвязей во временном ряду цен, лежащая в основе так называемой “мартингальной модели” (martingale model)*, предполагает отсутствие автокорреляционных взаимосвязей между приростом цен при любых сдвигах.
Случайный процесс Yt, t=1,2,..., характеризующий динамику цены в этом случае удовлетворяет следующему условию:
M=Yt, (7.16)
которое эквивалентно соответствующему условию для приростов цен
M=0. (7.17)
Выражения (7.16) и (7.17) свидетельствуют о том, что условное математическое ожидание цены в момент t+1 при известных ее значениях в периоды времени t, t–1, t–2,... равно ее значению в момент t, которое , в свою очередь, предопределено предшествующей динамикой этой цены или, что эквивалентно, условное математическое ожидание прироста цены за интервал (t, t+1) при известной ее предыстории равно нулю и, таким образом, прирост цены не зависит от предшествующих уровней цен. Последнее допущение также означает, что любые (по величине лага) непересекающиеся во времени приросты цен некоррелированы между собой, что предопределяет невозможность их предсказания с помощью линейных моделей временных рядов, рассмотренных в главе VI. Таким образом, “лучший прогноз” цены на дату t+1– это ее уровень на дату t.
Условия (7.16) и (7.17) удовлетворяют предпосылкам так называемого “эффективного рынка”, одна из важнейших среди которых свидетельствует о том, что текущая цена полностью предопределена информацией, содержащейся в ценах предыдущих периодов и не существует никакой другой информации, поступившей в период (t, t+1), эксклюзивное владение которой позволяет участникам торговых сделок извлечь дополнительную прибыль. Следовательно, условное математическое ожидание прироста цены на ее предшествующие значения не может быть ни положительным, ни отрицательным, а “обязано” быть равным нулю, и изменения цены являются абсолютно случайными и непредсказуемыми.
С точки зрения “ортогонального” условия (7.15) предпосылки мартингальной модели означают, что функция f является линейной с аргументом, выражающим прирост цен в текущем периоде, а функция g может быть любой по отношению к этому аргументу, рассматриваемому в предшествующие периоды. Кроме линейной функции прироста в качестве g может рассматриваться, например, любая степенная функция от этого аргумента, т. е. g(Dyt–k2), g(Dyt–k3),... , k=1, 2,... .
Достаточно широкий класс моделей финансовой эконометрики базируется на предположении о том, что приросты цен эквивалентны случайному процессу по своим свойствам близкому к “белому шуму”. Это предположением отражает сущность так называемой “гипотезы случайного блуждания” (ГСБ). В научной литературе описаны три версии этой гипотезы, которые отличаются друг от друга содержанием, вкладываемым в понятие “белого шума”.
Согласно первой версии этой гипотезы – ГСБ-1, разработанной еще в начале ХХ века*, случайные приросты финансового показателя (цены) и любые их функциональные преобразования независимы и удовлетворяют условию стационарности или иначе имеют идентичные условные распределения на уровни цен в прошедшие моменты времени. Таким образом, ГСБ-1 утверждает, что динамика приростов цены по своим свойствам соответствует процессу “строгого белого шума”. Как правило, закон распределения приростов предполагается нормальным N~(0, s2), в специальных случаях – стабильным**.
С точки зрения выражения (7.15) это означает, что в качестве f(zt) и g(zt–k) могут рассматриваться как линейные, так и степенные функции от приростов z (например, квадраты и более высокие степени).
Вместе с тем, результаты анализа динамики многих финансовых показателей, зафиксированных на мировых рынках, свидетельствуют, что продекларованное ГСБ-1 предположение об идентичности закона распределения их приростов часто не подтверждается, особенно на продолжительных (свыше года) периодах наблюдения. В значительной степени это относится к параметрам их закона распределения (обычно к дисперсии), хотя вид этого закона может и не изменяться. Например, дисперсия не удовлетворяет условию гомоскедастичности и меняется во времени.
Процесс с независимыми, но неодинаково распределенными (имеются в виду условные распределения на уровни цены в прошлом) приращениями, вообще говоря, не относится к разряду процессов “белого шума”, поскольку в данном случае он не является стационарным (точнее, не удовлетворяет условиям стационарности 2-го порядка). Вместе с тем , отказ от идентичности закона распределения приростов является логичным развитием ГСБ-1, “смягчающим” ее достаточно строгие ограничения в отношении свойств приростов цены.
Предположение о независимости приростов цены и неидентичности их условных распределений выражает сущность второй версии ГСБ – ГСБ-2. Таким образом, ГСБ-2, как ГСБ-1, предполагает, что как сами приросты, так и любые их функции независимы между собой. С точки зрения (7.15) это означает, что функции f(zt ) и g(zt–k ) также не ограничены по форме. Они могут быть как линейными, так и степенными. ГСБ-2 была обоснована уже во второй половине ХХ века*.
Смягчение условия полной независимости процесса приращений цен приводит к третьей версии ГСБ – ГСБ-3, согласно которой автокорреляционные связи между приростами отсутствуют, однако автокорреляция между их степенями может иметь место. Например, Cov(zt2), g(zt–k2))¹0, для некоторых сдвигов k¹0. Таким образом, с точки зрения выражения (7.15), функции f(zt) и g(zt–k ) являются по форме линейными от приростов z.
Формально, если при этом sz2=const, то такой процесс остается стационарным. Его свойства эквивалентны свойствам “слабого белого шума” – стационарного процесса с независимыми значениями. Такой процесс можно рассматривать как частный случай стационарного процесса второго порядка с нулевыми автокорреляциями.
Один из вариантов модели, соответствующей любой из рассмотренных версий ГСБ, может быть записан в следующем виде:
![]()
где m – ожидаемое постоянное изменение цены в период (t–1, t)**, t=1, 2,...; et – случайный прирост цены в интервале (t–1, t), свойства которого удовлетворяют одной из версий ГСБ. С целью сохранения преемственности в терминологии, по-прежнему, et будем называть ошибкой. Обычно при всех версиях ГСБ предполагается, что et~N(0, se2), либо она распределена по стабильному закону с нулевым средним.
Для ГСБ-1 se2=const, для ГСБ-2 se2=st2, что означает изменчивость дисперсии во времени, но в то же время ряды et2, et–12, et–22,... являются статистически независимыми. При ГСБ-3 в отношении se2 могут быть выдвинуты различные предположения.
Рассмотрим некоторые общие закономерности динамики цены, вытекающие из выражения (7.18).
Подставляя в (7.18) последовательно значения t=1,2,... получим следующую последовательность значений цен:
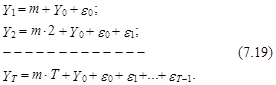
В силу независимости ошибок e0, e1, e2,... и равенства нулю их математического ожидания из последовательности (7.19) непосредственно вытекает, что при m¹0 условное математическое ожидание цены в момент Т на ее значение Y0, зафиксированное в момент t=0, является линейной функцией от времени
M=Y0+m×Т. (7.20)
Аналогично, в силу независимости ошибок et, t=1, 2,...; несложно показать, что условная дисперсия цены YT на ее значение Y0 определяется как сумма квадратов ошибки e.
D(YТ/Y0)=M2=M2=
![]() *
. (7.21)
*
. (7.21)
Для ГСБ-1, в частности, из выражения (7.21) вытекает, что в силу равенства M=M=...=se2, условная дисперсия D(YТ/Y0) с ростом t также растет во времени согласно линейному закону
D(YТ/Y0)=se2×Т. (7.22)
В случае ГСБ-2 правая часть выражения (7.22) примет вид ![]()
Из выражений (7.20)–(7.22), в частности, вытекает, что при m=0 условное математическое ожидание M =const, а условная дисперсия, как и в общем случае, увеличивается согласно линейной зависимости.
Неограниченность роста условной дисперсии (7.21) в общем случае противоречит очевидному условию неотрицательности цены в любой момент времени, т. е. Yt³0, t=1, 2,... С целью избежания этого противоречия, там, где оно может иметь место, модели финансовой эконометрики “работают” или с логарифмами цены yt=lnYt, или с логарифмами доходов ![]()
В этих случаях аналогами модели (7.18) являются следующие выражения соответственно:
![]()
![]()
где показатели m и et имеют то же статистическое содержание, что и показатели m и et в модели (7.18), т. е. являются математическим ожиданием и ошибкой соответственно.
Знание специфических свойств процесса изменения финансового показателя позволяет подобрать (построить) адекватную его закономерностям математическую модель, которая более точно описывает исходный ряд Yt, а, следовательно, и обладает лучшими предсказательными способностями в отношении его будущих значений Yt+1, Yt+2,... по сравнению с другими вариантами моделей.
Выявление этих свойств прежде всего предполагает умение соотносить свойства рассматриваемого процесса с какой-либо из версий ГСБ. Решение этой непростой проблемы обычно осуществляется с помощью специальных тестов, которым подвергается исходный ряд цен Yt, t=0, 1, ... или какие-либо его производные характеристики (доходы, логарифмы цен, их приросты и т. п.).
Поможем написать любую работу на аналогичную тему

