Обобщая изложенный в главе VII материал, отметим, что в предыдущих разделах были рассмотрены модели с линейной структурой условного математического ожидания, в которых этот показатель был выражен в виде линейных функций, соответствующих процессам АР(k), СС(т), АРСС(k, т). Дальнейшее развитие аппарата моделирования временных рядов финансовых показателей связывается с построением моделей с нелинейными структурами (“нелинейных моделей”), как для математического ожидания, так и для дисперсии.
Заметим, что в общем случае можно предполагать, что класс моделей с нелинейными структурами должен быть значительно шире по своему составу, чем класс “линейных” моделей. Вследствие этого в данном разделе рассматриваются принципы построения лишь некоторых групп “нелинейных” моделей, которые были разработаны специалистами в области финансовой эконометрики в последнее десятилетие.
Основная идея одного из подходов к построению нелинейных моделей временных рядов финансовых показателей заключается в представлении ряда цен Yt в виде нелинейной функции, аргументами которой являются текущее и предшествующие значения стандартизованной случайной переменной et, свойства которой соответствуют белому шуму, et ~N(0, 1), M=0, i >0.
При этом обычно в выражении (7.162) используется функция f(.), образованная суммой двух функций, одна из которых выражает условное математическое ожидание переменной Yt на прошлые значения ошибки, а другая – условную дисперсию:
где функции g(.) и h(.) могут быть как линейными, так и нелинейными.
На основании (7.173) несложно заметить, что условное математическое ожидание Yt определяется как M=g(et–1,et–2,...) в силу свойств переменной et (M=0, M=0, i=1,2,...), а условная дисперсия D(Yt/et–1,et–2,...)=M2= =M×Mk = M×hk(.).
Выражение (7.173) можно рассматривать как результат разложения функции (7.172) в ряд Тейлора в точке et=0 при заданных значениях et–1, et–2, ...
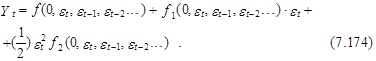
Пренебрегая в выражении (7.174) слагаемыми, содержащими etk, k>1, получим, что g(et–1, et–2,...)=f(0, et–1, et–2,...), h(et–1, et–2,...)= =f1(0,et–1 , et–2,...).
Из вида уравнения (7.173) также следует, что все множество нелинейных моделей финансовых показателей может быть разделено на две группы: модели с нелинейным условным математическим ожиданием и модели с нелинейной условной дисперсией.
Примером модели с нелинейным условным математическим ожиданием является следующее уравнение:
в котором g(.)=a1 et–12 и h(.)=1.
Из выражения (7.175) непосредственно видно, что условное математическое ожидание M=a1et–12 является функцией от квадрата предыдущей ошибки, а условная дисперсия равна единице M=1.
Напротив, модель типа ARCH первого порядка , предложенная Энглом в 1982 г., характеризуется нелинейной условной дисперсией. Ее уравнение имеет следующий вид:
В данном случае условное, как и безусловное математическое ожидание равно нулю, g(.)=0, и функция h(.) определяется выражением 
, так что условная дисперсия D(Yt/et–1,et–2, ...)=
также зависит от квадрата предыдущего значения ошибки.
Таким образом, вообще говоря, модели с изменяющейся зависимой вариацией можно рассматривать как модели с нелинейной условной дисперсией.
Модели с нелинейными условными математическими ожиданиями и модели с нелинейными условными дисперсиями описывают временные ряды финансовых показателей, имеющие принципиально различные свойства. Они определяются в основном отличиями их третьего и четвертого моментов.
Так, например, процессы, соответствующие моделям (7.175) и (7.176), имеют нулевые автокорреляционные функции. В самом деле, в случае (7.175) первая автоковариация определяется следующим выражением:
Для процесса, соответствующего модели (7.176) имеем тот же результат:
Вместе с тем можно показать, что начальные моменты порядков, начиная с третьего, у моделей с нелинейными условными математическими ожиданиями отличны от нуля, т. е. 
Например, для третьего момента модели (7.175) имеем
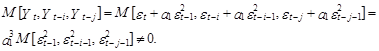
Вместе с тем, такие моменты для модели с нелинейной условной дисперсией равны нулю, В частности, для модели (7.176) имеем
в силу независимости случайных переменных 
Однако некоторые четные моменты процессов, адекватных моделям с нелинейной условной дисперсией, начиная с четвертого, при равенстве пар индексов становятся отличными от нуля. В самом деле, для модели (7.175) при i=0, j=k=1 имеем
Подобные свойства моментов позволяют предложить достаточно универсальные тесты для определения соответствия реального процесса той или другой группе нелинейных моделей. Подобные тесты, например, могут быть основаны на проверке значимости нормированного третьего момента временного ряда Yt при i>j>0. Такой момент определяется следующим выражением:
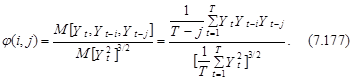
При j(i, j)=0, что соответствует процессам с нелинейной дисперсией, расчетное значение 
распределено приблизительно по нормальному закону с нулевым средним и дисперсией, определенной следующим выражением:
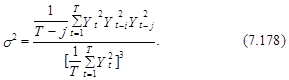
С учетом выражений (7.177) и (7.178) реальный процесс можно считать соответствующим модели с нелинейной условной дисперсией, если выполняется следующее соотношение*:
Для моделей с нелинейными условными математическими ожиданиями в общем случае можно предложить несколько вариантов формирования функции g(et–1, et–2, ...).
Во-первых, можно выразить эту функцию в виде полинома от стандартизованной случайной переменной 
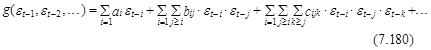
В случае bij =cijk =0 имеем модель с линейным условным математическим ожиданием.
Во-вторых, функцию g(et–1, et–2,...) можно выразить в виде нелинейной модели авторегрессионного вида
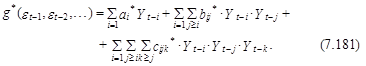
В-третьих, возможно функцию g представить смешанным уравнением типа авторегрессии-скользящего среднего
Для моделей каждого типа могут быть подобраны соответствующие методы оценки их параметров.
Поможем написать любую работу на аналогичную тему