Для описания процессов с редкими скачками вариации, вызванными в основном экстраординарными событиями, обычно используются модели, в которых дополнительно к выражению (7.101) вводится ограничение на вероятность такого скачка в произвольный момент времени t. Обычно предполагается, что р(M=M)=a, где a®1. Иногда количество скачков за определенный период времени (например, за год) предполагается постоянным.
Примером такого типа моделей является модель с марковской вариацией. Она формируется на основе следующих предпосылок.
Предположим, что переменная vt может принимать только два значения s1 и s2, каждое с вероятностью 1/2, t=1,2,... . И в каждый момент времени t существует вероятность (1–a), что текущее значение этой переменной может поменяться на альтернативное, т. е. вероятность того, что s1 изменится на s2 и, наоборот, равна (1–a), где a – величина, близкая к 1, a<1. Обозначим
![]()
где, как и ранее, процессы vt и ut независимы, и ut – строгий белый шум, ut ~ N(0,1).
Несложно показать, что процесс хt обладает нулевой автокорреляционной функцией, начиная с первого коэффициента, т. е. по своим свойствам он близок к белому шуму. В самом деле, в силу независимости процессов ut и ut–i, i =1,2,... имеем
![]()
Вообще говоря, значения дисперсии этого процесса на различных временных отрезках могут различаться между собой. Вместе с тем, заметим, что в общем случае значение безусловной дисперсии процесса хt определяется следующим выражением:
![]()
Выражение (7.106) можно получить, отталкиваясь от понятия условной дисперсии случайной величины хt при известных значениях vt–1, vt–2,... (D(хt/vt–1, vt–2,...)), величина которой определяется следующим образом:
![]()
Выражение (7.107) было получено с учетом того, что если в момент t–1 случайная переменная vt–1 была равна s1, то р(vt=s1)=a, а р(vt =s2)=1–a и наоборот, если vt–1 была равна s2, р(vt=s2)=a, а р(vt=s1)=1–a .
На основании этого (7.107) можно переписать в следующем виде:
![]() D(xt / vt - 1) =
D(xt / vt - 1) = 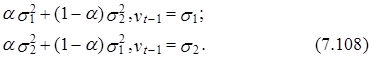
Из выражения (7.108) в частности, вытекает, что условные дисперсии рассматриваемого процесса хt различаются между собой.
С учетом того, что р(vt–1=s1)=р(vt–1=s2)=1/2 из (7.108) непосредственно следует выражение (7.106):
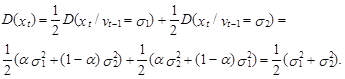
Важной характеристикой, которая позволяет идентифицировать процессы, соответствующие модели (7.101) с редкими скачками вариации, является автокорреляционная функция процесса хt2. В общем случае значение i-го коэффициента автокорреляции ri(хt2) определяется следующим образом:
![]()
где ![]()
Четвертые моменты переменной хt, входящие в выражение (7.109), с учетом (7.103) получим для i=1 следующим образом:
![]()
![]()
![]()
При выводе выражения (7.111) учтено, что
1) коэффициент эксцесса случайной переменной ut, распределенной по нормальному закону, равен 3. При этом его величина для переменной ut рассчитывается согласно следующему выражению:
![]()
поскольку ut~N(0,1), то из (7.112) непосредственно следует, что M=3;
2) значение M определяется с учетом равновероятных событий vt=s1 и vt=s2 как
![]()
Подставляя все известные моменты случайной величины хt2 в выражение (7.109), после несложных преобразований получим:
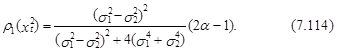
При получении второго коэффициента автокорреляции процесса хt2 – r2(хt2) необходимо анализировать различные варианты последовательностей vt, vt–1, vt–2 с учетом того, что переменная vt может принимать только значения s1 иs2. Опуская достаточно громоздкие выражения, приведем окончательное выражение этого показателя
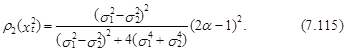
Далее также можно показать, что значение i-го коэффициента автокорреляции процесса хt2 определяется общей формулой
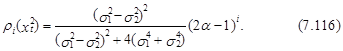
Из выражений (7.114)–(7.116) непосредственно следует, что при a®1 для коэффициентов автокорреляции любого порядка процесса хt2 справедливо следующее соотношение:
![]()
Из выражений (7.114) и (7.115) непосредственно следует, что
![]()
Значения s1 иs2 могут быть определены, например, из уравнений (7.106), (7.110) или (7.111) при рассчитанных для ряда хt значениях M, M и M.
Как это было показано в главе VI (см. раздел (6.5)), выражение (7.116) позволяет считать процесс хt2 адекватным АРСС(1,1) с малыми, но медленно спадающими значениями коэффициентов автокорреляции.
Поможем написать любую работу на аналогичную тему

