Модели процессов с зависимой вариацией

Привязка изменений вариации цен к экстраординарным событиям не выглядит достаточно реалистично, хотя бы по той причине, что такого рода события возникают достаточно редко и они не в полной мере объясняют весь спектр этих изменений. Многие менее значительные события, какая-либо информация также воздействуют на цены, изменяя их пусть и на незначительную величину. Вместе с тем, подобная информация поступает на рынок практически непрерывно и в результате ее наложение может вызвать и достаточно сильные колебания в уровнях цен даже в течение одного дня. Это позволяет считать условную вариацию процесса Yt  случайной величиной, значения которой в моменты t=1,2,... зависят от некоторых других переменных, отражающих сложившуюся на рынке текущую ситуацию.

В таком случае процесс vt, отражающий стандартные отклонения в уровне цен, может обладать более широким спектром закономерностей, по сравнению с рассмотренными выше. В научной литературе выдвинут целый ряд гипотез в отношении переменной vt. Основными из них являются следующие две, отражающие ГСБ-3, t=1,2,... Первая гипотеза предполагает, что значения vt  представляют собой условное стандартное отклонение, являющееся детерминированной функцией от прошлых значений цен:

vt=f(Yt–1, Yt–2,...).                         (7.118)

В качестве примера такой функции может рассматриваться следующее выражение:

где коэффициенты a 0  и a1 являются положительными.

Вторая гипотеза предполагает независимость условного стандартного отклонения от уровня цен, но допускает, что переменная vt  может быть представлена функцией типа уравнения авторегрессии-скользящего среднего

vt=j(vt–1, vt–2,..., ht),                         (7.120)

ставящей ее уровень в момент t в зависимость от ее значений в прошедшие периоды времени и случайной составляющей ht. Случайную составляющую ht  будем отличать от ошибки et, присутствовавшей в моделях цены, хотя их статистические свойства идентичны, ht~N(0, sh2), et=Yt–m(t), et ~N(0, se2).

В отношении переменной ut  будем придерживаться предположения о том, что это – процесс строгого белого шума.

Выражения (7.118) и (7.120) предполагают, что во временных рядах квадратов отклонений цен от их среднего уровня существуют корреляционные взаимосвязи. Модели с такого рода взаимосвязями получили название ARCH-моделей  (Autoregressive Conditionally Heteroskedastic models).

Общий вид ARCH-модели, построенной на основе выражения (7.119), может быть представлен следующим уравнением:

Для k=1 в соответствии с выражением (7.119) получим

Все коэффициенты a 0, a 1,..., ak  в выражениях (7.121) и (7.122) являются неотрицательными*.

Из выражения (7.122), в частности, следует , что условная дисперсия цены в момент t D(Yt/Yt–1) при известном значении Yt–1  определяется как

Таким образом, согласно (7.123) большие отклонения цен от математического ожидания в день t влекут за собой увеличение дисперсии в ценах следующего периода и, наоборот, уменьшение отклонений влечет за собой снижение величины этой дисперсии.

Из выражения (7.123) также вытекает, что переменные vt2 и ut–12 не являются статистически независимыми. Это следует из того, что vt2=D(Yt /уt–1) зависит от (Yt–1–m)2 =vt–12×ut–12.

Из выражений (7.121) и (7.122) непосредственно вытекает, что свойства автокорреляционных функций процесса (Yt–m)2 в первом случае должны соответствовать процессу АР(k), а во втором – удовлетворять следующему соотношению ri(st)=a1i, где st=(Yt –m)2.

Представление стандартного отклонения vt  в виде функции типа (7.120) основано на том, что отклонение цены актива за t-й день торговли от ее среднего уровня может быть представлено в виде суммы приростов цен в ходе торговых сделок, имевших место в этот день

В выражении (7.124) переменные wit   и Nt являются случайными. Причем wit   означает изменение цены в ходе i-й сделки в течение t-го дня, а Nt  выражает общее количество таких сделок.

Предположим, что wit  независимы и одинаково распределены по нормальному закону с нулевым математическим ожиданием и дисперсиейsw2, wit~N(0, sw2) и также независимы от переменной Nt. Тогда при фиксированном числе сделок условное стандартизованное отклонение может быть определено как  vt =sw2

В предположении, что цены  не влияют на переменную vt можно записать*

Поскольку , как сумма одинаково распределенных по нормальному закону случайных величин, также имеет нормальное распределение, причем  то очевидно, что переменная ut распределена по  стандартизованному нормальному закону, ut ~N(0, 1). Из построения переменной ut, t=1,2,... также вытекает, что распределение ее значений, является одинаковым для всех vt и переменные ut, ut–i   являются  статистически независимыми между собой и с переменными vt  и vt–j   для всех сдвигов i и j. Иными словами, процесс иt  можно  считать по крайней мере белым шумом.

Отметим основные свойства процессов vt  и vt 2. В частности, заметим, что если  ut   является белым шумом, то процесс ut=Yt –m  также является белым шумом в силу условия (7.105). Однако значения st=(Yt –m)2=хt2× могут коррелировать между собой в случае коррелированности значений переменной vt2 и vt–i2, i=1,2,... . Это непосредственно следует из определения ковариации и математического ожидания произведения переменных vt 2   и st  соответственно

и

При выводе этих выражений учтено, что  (см. (7.103)).

Из выражения (7.127) непосредственно вытекает, что

В частности, при положительной автокорреляции процесса условной вариации vt2 можно показать, что коэффициенты автокорреляции процессов vt2   и st   удовлетворяют следующему соотношению:

Соотношение (7.129) непосредственно вытекает из того, что

и Ku=3, если ut  ~N(0, 1).

В свою очередь, при получении выражения (7.130) учтено, что

где Ku  – коэффициент эксцесса процесса ut   определяется как

Для оценки параметров процесса vt2 можно использовать также и характеристики неотрицательного процесса абсолютных отклонений цен от своего среднего уровня zt=ïYt–mï=ïхtï. Для этого процесса при vt >0  получим

Очевидно, что

Из определения zt  процесса также вытекает следующая взаимосвязь между его ковариациями и ковариациями процесса vt:

Из выражения (7.133) непосредственно следует, что коэффициенты автокорреляции процессов zt и vt  связаны следующим соотношением:

Далее, выражая дисперсии через второй начальный момент и математическое ожидание, увидим, что *.  Из этого факта вытекает следующее соотношение для коэффициентов автокорреляции процессов zt  и vt :

Результаты (7.129) и (7.135) являются достаточно общими в пределах исходного ограничения vt>0, t=1,2,... . Однако на практике выполнение этого ограничения гарантировано не при всех типах распределения vt. Например, при нормальном распределении  vt~N(M, sv2) всегда существует вероятность того, что некоторые значения vt могут быть отрицательными. Таким образом, функция плотности распределения vt  должна быть определена только на положительной полуоси. Такую функцию плотности имеет, в частности, переменная, логарифм которой распределен по нормальному закону.

Предположим, что ln(vt)~N(a, b 2), b>0.  В этом случае функция плотности переменной vt   имеет следующий вид:

Тогда  в соответствии с выражениями (7.9) и(7.10) получим, что  и поскольку  то для всех начальных моментов переменной vt   имеем

С учетом (7.137), выражая дисперсию через второй начальный момент и математическое ожидание, получим, что

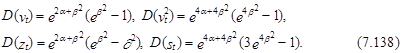
Далее, принимая во внимание, что для ut ~N(0, 1) , вместо условий (7.129) и (7.133) получим следующие соотношения для коэффициентов автокорреляции процессов st  и vt 2, zt  и vt :

Из (7.139), в частности, вытекает, что А(b) монотонно  увеличивается с ростом b от значения А(0)=0, до значения А(¥)=1/3. Аналогично ведет себя и В(b): В(0)=0, В(¥)=2/p.

Из выражений (7.139) и (7.140) также следует, что коэффициенты автокорреляции ri  (st) и ri (vt2), ri (zt) и ri(vt) должны быть одного знака, поскольку А(b) и В(b) являются неотрицательными числами. При этом многочисленные исследования реальных процессов показывают, что в случае стационарных процессов значения ri(st) и  ri(zt) для первых десяти сдвигов являются положительными. Из этого эмпирического факта следует, что коэффициенты  ri(vt 2) и ri(vt) также являются положительными.

В том случае, если процесс ln(vt) представлен моделью авторегрессии первого порядка :

где a – математическое ожидание процесса ln(vt), ln(vt)~N(a, b2);   ht ~N(0, sh2) – ошибка модели, являющаяся процессом белого шума, sh2=D(b2)×(1–a12); a1=r1(ln(vt))– коэффициент модели, то можно показать, что  коэффициенты автокорреляции процесса ln(vt) и коэффициенты автокорреляции процесса vt   связаны следующим соотношением:

Для процесса vt2, чтобы получить соответствующие выражения для коэффициентов автокорреляции достаточно в правой части (7.142) b 2   заменить на 4b 2.

Далее, поскольку коэффициенты автокорреляции модели (7.141) равны a1i (ri(ln(vt ))=a1i), то соответствующие коэффициенты процессов st  и zt   на основании (7.139) и (7.140) будут определяться следующими выражениями:

и

Выражения (7.143) и (7.144) показывают, что эти коэффициенты с увеличением сдвига монотонно уменьшаются с некоторого значения меньшего 1 до нуля.

Дальнейшее направление разработок моделей с изменяющейся зависимой вариацией связывается с подбором более удачной модели для описания динамики переменной vt в тех случаях, когда количество параметров в авторегрессионных версиях достаточно велико. Напомним, что авторегрессионные версии моделей этой переменной могут быть представлены, например, следующими выражениями:

Коэффициенты этих и других возможных вариантов моделей такого типа определяются на основе коэффициентов автокорреляции процессов st  и zt, t=1,2,..., значения которых являются неотрицательными, но достаточно небольшими и стремятся к нулю с увеличением сдвига. Как отмечалось в главе VI, при k>2 относительные погрешности эмпирических коэффициентов автокорреляции могут быть достаточно большими, что повлечет за собой и ошибки коэффициентов модели.  В результате построенная модель не будет достаточно точно воспроизводить поведение процесса .

Избежать влияния погрешностей в оценках коэффициентов автокорреляции процессов st  и zt на точность представления переменной vt при больших сдвигах можно на основе использования при ее описании вместо авторегрессионных моделей (АР(k)) моделей более общего класса – авторегрессии-скользящего среднего (АРСС(k, m)) с гораздо меньшим числом параметров. В частности, в главе VI было показано, что добавление к модели авторегрессии первого порядка модели скользящего среднего первого порядка позволяет сформировать модель, по своим свойствам эквивалентную модели авторегрессии достаточно высокого порядка. Такой подход, в частности, предполагает, что вместо модели (7.145) для описания процесса vt2, может быть использована, например, модель следующего вида:

связывающую текущее значение условной дисперсии с ее предшествующим значением и предшествующим квадратом ошибки , определяемой по отклонению цены актива в момент t–1 от ее математического ожидания.

Модели типа (7.146) в научной литературе получили название GARCH моделей (Generalized Autoregressive Conditionally Heteroskedastic models).  Общий вид  GARCH модели порядка   (k, r) может быть определен следующим выражением:

Коэффициенты модели (7.147) в общем случае должны быть неотрицательными, чтобы гарантировать выполнение естественного условия vt2>0. Это ограничение не совсем удобно обеспечивать при оценке параметров модели (7.147) традиционными методами. Кроме того, в GARCH–моделях условная дисперсия зависит лишь от размера отклонения цены от ее математического ожидания, а не от ее знака. Вместе с тем эмпирические данные (реальные временные ряды цен), свидетельствуют, что их вариация и доходность часто имеют отрицательную корреляцию. Иными словами, с ростом цен активов, обеспечивающим увеличение их доходности, условная вариация ряда Yt  уменьшается, и, наоборот, с уменьшением цен и соответственно снижением доходности – вариация растет. В результате периоды высокой вариации обычно совпадают с периодами спадов на финансовых рынках, а периоды низкой вариации с периодами роста активности на них. Такие закономерности учитываются, например, модификацией GARCH-модели, уравнение которой в общем виде может быть представлено следующим выражением:

Согласно модели (7.148) условная дисперсия в момент t является асимметричной функцией от положительных и отрицательных значений ошибки et–i=Yt–i–mt–i, i=1,2,..., где mt–i  – условное математическое ожидание в момент t–i.  Иными словами, положительные и отрицательные значения ошибки et–i оказывают различное влияние на зависимую переменную. Кроме того, использование в модели логарифма дисперсии позволяет не беспокоиться о знаках коэффициентов данной модели.

Дальнейшее развитие ARCH-модели связывается с предположением о существовании зависимости значений уt  от их условной вариации. Класс этих моделей, названный ARCH-М моделями, отражает мнение, что на финансовых рынках покупатели как бы “требуют” компенсации за рискованные вложения. В результате “плата за риск” рассматривается как возрастающая функция от условной вариации цены акции.

Простейший вариант ARCH-М модели, отражающий данное предположение, может быть представлен в следующем виде:

где условное математическое ожидание цены актива mt=Mt–1, в свою очередь, ставится в зависимость от условной вариации ошибки согласно следующему выражению:

и vt2  является ARCH-процессом:

В более общем случае условная вариация ошибки может быть представлена в виде GARCH-процесса:

где, напомним, et=уt–mt.

Тестирование моделей типа ARCH и GARCH обычно  сводится к проверке существования характерных для них эффектов. Для этих целей, как правило, используется так называемый критерий TR2, где T – объем выборки и R2 – коэффициент детерминации соответствующей модели для квадрата ошибок (например, типа (7.145) и (7.146)). Этот показатель распределен по закону c2  с числом степеней свободы равным количеству используемых в модели лаговых переменных et–i  и vt–j. Если расчетное значение TR2>c2*(р*, n), где р* – заданный уровень доверительной вероятности и n – число степеней свободы, то гипотеза о присутствии ARCH или GARCH-эффектов принимается, в противном случае она отвергается. Здесь следует отметить, что наличие эффекта в данном случае связывается со значимостью коэффициентов ai  и bj, i=1,2,..., k; j=1,2,..., n; модели, описывающей взаимосвязи между квадратами ошибки. Если TR2>c2*(р*, n), то коэффициенты принимаются значимыми, т. е. отличными от нуля (по крайней мере, некоторые из них), и в этом случае допускается наличие эффекта типа ARCH или GARCH (условная дисперсия меняется согласно соответствующей закономерности). В противном случае, т. е. когда TR2£c2*(р*, n), следует принять гипотезу о равенстве нулю всех коэффициентов при лаговых значениях квадрата ошибки, и в этом случае дисперсия должна рассматриваться как постоянная величина.