Тестирование финансовых процессов

Для выявления соответствия свойств реального финансового процесса какой-либо из версий гипотезы случайного блуждания, каждая из которых в свою очередь характеризуется специфической формой ортогонального условия (7.15), обычно применяются специальные тесты. Поскольку финансовые процессы являются временными рядами, то в целом, группировка таких тестов аналогична группировке, рассмотренной в главе VI. Иными словами, все множество тестов разделяется на три группы: параметрические, полупараметрические и непараметрические. Более того, многие из рассмотренных в главе VI тестов могут быть использованы и в анализе финансовых процессов, разумеется с учетом их особенностей. Основными из них являются большая продолжительность временного ряда, что позволяет использовать асимптотические оценки; не обязательно нормальное распределение приростов (ошибки), что сужает возможности применения параметрических тестов.

Как и для временных рядов в целом при тестировании финансовых процессов достаточно широкое распространение получили непараметрические тесты, основанные на анализе закономерностей формирования серий последовательных значений финансовых показателей с одинаковым знаком и частот смены знаков у этих серий. Вместе с тем, в отличие тестов временных рядов, рассмотренных в главе VI, которые были ориентированы на выявление свойств случайности, стационарности, непараметрические тесты финансовых процессов нацелены на проверку более жесткого ортогонального условия (7.15), предполагающего отсутствие во временном ряду финансового показателя или в ряду его функциональных преобразований автокорреляционных связей.

Один из базовых непараметрических тестов, разработанный еще в 1937 г. Коулсом и Джонсом* для проверки ГСБ-1, анализирует закономерности формирования возрастающих и убывающих по величине последовательных значений временного ряда и смены направления этих изменений. Данный тест не достаточно  сильный. Более того, он в основном ориентирован на выявление автокорреляционных связей во временном ряду самого финансового показателя и, вследствие этого, даже в большей степени подходит для проверки других версий ГСБ – ГСБ-2 и  ГСБ-3.  Вместе с тем, его идеи оказались достаточно плодотворными и на их основе было развито целое направление тестирования ГСБ-1.

Дадим описание этого теста на примере модификации модели (7.23), оперирующей с логарифмами цен

где yt=lnYt; Yt  – уровень цены актива в момент t, и математическое ожидание его прироста равно нулю, m=0. Тогда ошибку модели (7.25) можно представить как разность последовательных значений показателя y

Значения  et  являются случайными величинами с нулевым математическим ожиданием. Они могут быть как положительными, так и отрицательными (включим в последнее множество и нулевые значения ошибки). Обозначим через It  случайную переменную, принимающую только значения 0 или 1 при следующих условиях:

 It  = 

Тест Коулса-Джонса основан на сопоставлении числа пар значений et, et+1  с  одинаковыми (положительными или отрицательными) знаками с количеством смен знаков во временном ряду  et . С этой целью с использованием соседних значений It  и It+1   сформируем величину Аt    согласно следующему выражению:

Аt=It ×It+1+(1– It)(1– It+1).                       (7.28)

Несложно убедиться, что на каждой паре It  и It+1   Аt   принимает значение либо 0 (если It  и It+1  имеют разные значения), либо 1 (если значения It  и It+1  совпадают). Тогда для любой последовательности et, t=0,1,2,..., Т, число NS, рассчитанное как

представляет собой количество пар значений ошибки et  и et+1, имеющих одинаковый знак, а число Nr , определяемое как

Nr = T – NS  –                                   (7.30)

количество смен знаков у ошибки.

Если ГСБ справедлива, то при m=0 и дополнительном предположении о симметричности распределения ошибки, числа NS и Nr  должны быть приблизительно равными, а, следовательно, и их отношение

будет достаточно близким к единице. При достаточно больших значениях Т этот вывод является следствием теоремы Чебышева, вытекающим из представления (7.31) в виде отношения частот pS=NS/Т и pr=Nr/Т, pS=1–pr, которые при Т®¥ определяют вероятности последовательностей et  и et+1   с одинаковым знаком и смены знаков у этих значений ошибки соответственно

где символ “” означает сходимость в вероятностном смысле случайной величины SR к ее математическому ожиданию, в данном случае равному единице.

Заметим, что NS   является случайной переменной, сформированной как сумма Т случайных величин Аt, распределенных по закону Бернулли на множестве 1 и 0. Закон распределения Аt  с ростом  Т приближается к нормальному. Причем, поскольку для ошибки, определенной по формуле (7.26), имеем      р(et>0)=р(et£0)=1/2, то из выражения (7.28) непосредственно вытекает, что

Из этого факта следует, что математическое ожидание величин NS  и Nr  равно

а их дисперсия –

Можно показать, (см. приложение 3 к главе VII), что в этом случае с увеличением Т закон распределения отношения           SR=NS/Nr  также является нормальным с математическим ожиданием, стремящимся к единице, и дисперсией отношения D(NS/Nr), асимптотически приближающейся к следующей величине:

Таким образом, проверка ГСБ с использованием теста Коулса-Джонса при небольших значениях Т состоит в установлении факта принадлежности расчетного значения NS /Nr следующему интервалу:

где t* (р*, Т–1)  – табличное значение критерия Стьюдента, соответствующее уровню доверительной вероятности р*    и числу степеней свободы Т–1.

При Т®¥  для этих же целей целесообразно использовать стандартизованное нормальное распределение, согласно которому ГСБ принимается, если выполняется следующее соотношение:

где пределы х1   и х2    находятся из равенства

р*=ò

(см. выражение (6.32)).

Если соотношение (7.37) выполняется, то временной ряд уt удовлетворяет ГСБ с вероятностью р*  .

Рассмотренный тест может быть усовершенствован и на более общий вариант модели (7.23), который, напомним, записывается в следующем виде:

где m¹0; et  – значение случайной ошибки, распределенной по нормальному закону, et ~N(0,  se2) .

В этом случае, поскольку m¹0, то случайная величина It, определенная согласно выражению, аналогичному (7.27), имеет другое соотношение вероятностей:

 It  =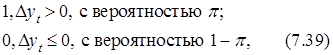 

где Dyt=yt–yt–1=m+et.

Очевидно, если m>0, то p>1/2, а при  m<0, p<1/2 .

В любом из этих случаев из выражения (7.28) вытекает, что вероятность pS  оказывается равной

а вероятность pr  определяется следующей величиной:

Тогда, очевидно, что соотношение этих двух вероятностей окажется больше единицы

Математическое ожидание случайной переменной NS,  как и в предыдущем случае определяется согласно распределению Бернулли, т. е. М=pS ×Т. Однако при определении дисперсии этой случайной величины следует учитывать, что в каждой паре переменные Аt  и Аt+1  зависимы между собой. В этом случае значение определяется следующим выражением

где ковариация двух последовательных случайных величин Аt  и Аt+1 рассчитывается согласно следующей формуле (см. приложение  1 к главе VII):

Коулс и Джонс показали, что случайная переменная SR из выражения (7.42) при больших значениях Т распределена приблизительно по нормальному закону с математическим ожиданием и дисперсией, определяемыми следующими выражениями соответственно (см. приложение 3 к главе VII):

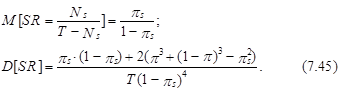
Заметим, что в тех случаях, когда в модели (7.38) постоянная составляющая прироста равна нулю, т. е. m=0, параметры распределения случайной величины SR, определенные выражением (7.45), равны 1 и 4/Т соответственно (см. выражение (7.36)).

С учетом выражения (7.45) тест Коулса-Джонса для проверки ГСБ состоит в следующем. Для модели (7.23) на основании временного ряда значений уt, t=1,2,...,Т, представляющих собой логарифм цены актива Yt, т. е. yt=lnYt, определяются: а) постоянная составляющая прироста m и б) временной ряд ошибки  et. Заметим, что m является средним приростом значений уt, т. е.

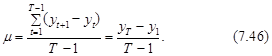
В предположении, что ряд ошибки et  распределен по нормальному закону с нулевым средним и дисперсией se2=s2, т. е. et~N(0,se2) можно оценить вероятность события It =1, т. е. значение  p, согласно следующему выражению:

p=р(et >0)=ò

где f(х) – плотность стандартизованного нормального распределения и F(m/s)– табличное значение интеграла вероятностей.

Подставив найденное значение p  в выражение (7.45) непосредственно получим теоретические значения параметров распределения отношения SR. Если его расчетная (эмпирическая) величина, определяемая как , где  и At определено выражением (7.28), и It  –  выражением (7.27), удовлетворяет соотношению

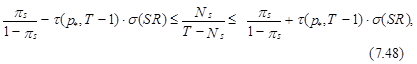
то ГСБ принимается с вероятностью р* , где t(р* , Т–1)– табличное значение критерия Стьюдента, соответствующее доверительной вероятности р*   и числу степеней свободы Т–1 ; s(SR) определяется как корень из дисперсии , в свою очередь, рассчитанной согласно (7.45).

В научной литературе описано целое семейство тестов ГСБ, основанных на прямых методах выявления корреляционных связей при различных лагах, как в самих временных последовательностях, так и во временных рядах функциональных преобразований их значений. Такие тесты, например, предполагают оценку значимости коэффициентов автокорреляции временных последовательностей логарифмов цен yt=lnYt, ошибок et  в моделях типа (7.23) и других в предположении, что случайная величина, представляющая собой коэффициент автокорреляции i-го порядка, i=1, 2,... k, при больших значениях Т распределена по стандартизованному закону нормального распределения, т. е. ri ~, где  ~D(ri ) (см. главу VI, выражения (6.25), (6.26)...). Тогда переменная  распределена по стандартизованному нормальному закону с нулевым средним и единичной дисперсией ~. В этом случае тест заключается в проверке значимости первых k коэффициентов автокорреляции. Если в ходе тестирования подтверждается их незначимость, то ГСБ принимается.

Для этих же целей может быть использован совокупный критерий согласия Бокса-Пирса (см. выражение (6.116), глава VI). Напомним, что случайная величина Qk , рассчитываемая как

при больших Т распределена по закону  c2(k). В соответствии с этим гипотеза об отсутствии автокорреляции в рассматриваемом временном ряду принимается, если выполняется следующее соотношение

Qk < c2(p*  , k).                                       (7.50)

Заметим, что при небольших значениях Т величину критерия Qk  рекомендуется определять согласно следующей формуле:

Учет некоторых других свойств временного ряда финансового показателя, соответствующих ГСБ, наряду с отсутствием автокорреляционных связей позволило сконструировать несколько более эффективные тесты проверки ГСБ по сравнению с “чисто автокорреляционными” тестами. Одним из основных среди этих свойств является линейная зависимость условной дисперсии временного ряда от времени (см. выражение (7.22)). Как уже отмечалось, это свойство в большей степени характерно для ГСБ-1. Однако и в случае других версий ГСБ характерно, что дисперсия суммы значений временного ряда равна сумме дисперсий каждого из них (см. выражение (7.21)).

В такой ситуации можно ожидать, что в условиях справедливости предположений ГСБ дисперсия суммы двух последовательных значений временно ряда qt  и qt–1  будет приблизительно равна удвоенной дисперсии значения qt  (см. выражение (7.5)). Напомним, что поскольку , то

Обозначим сумму qt+qt–1  как qt (2), т. е. qt (2)=qt+qt–1,  и составим отношение дисперсий значений qt (2) и удвоенной дисперсии значений исходного ряда qt, t=1, 2,..., Т; которое обозначим как VR (2). Получим

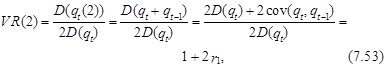
где r1 – первый коэффициент автокорреляции ряда qt.

В случае справедливости ГСБ можно ожидать, что поскольку r1®0, то отношение дисперсий будет близко к единице, т. е. VR(2)®1. При этом, если во временном ряду qt   имеет место  положительная автокорреляционная связь, то VR(2)>1. С точки зрения выражений (7.21) и (7.22) это означает, что условная дисперсия суммы двух последовательных значений временного ряда qt будет нарастать быстрее, чем по линейному закону. При отрицательной автокорреляции (r1<0) VR (2)<1, т. е. рост дисперсии этой суммы будет медленнее линейного закона.

Для построения теста, проверяющего ГСБ на основании отношения дисперсий VR(2), необходимо знать закон распределения этой случайной величины. Интуитивно на основании выражения (7.52) можно ожидать, что закон распределения VR(2) совпадает с распределением случайной переменной 2r1, которое, как было отмечено в главе VI, при r1®0 приблизительно нормальное с математическим ожиданием, равным нулю, и удвоенной дисперсией. Напомним, что дисперсия случайной переменной r1 (D(r1))  приблизительно равна 1/Т. В нашем случае можно ожидать, что ее величина составит 2/Т, т. е. D(2r1)=2/Т. Иными словами, случайная величина оказывается распределенной согласно нормальному закону , а величина  распределена по стандартизованному нормальному закону.

Для более строгого доказательства этого интуитивно предполагаемого результата рассмотрим процесс, определенный выражением (7.23), в моменты времени t=0,1,2,...,2Т. Оценки параметров математического ожидания постоянного прироста m и дисперсии D(y)=sy2 определим согласно следующим выражениям:

Заметим, что оценка дисперсии sy2   – s22 получена на основании четных значений ряда уt, т. е. для двойного периода времени между наблюдениями (t, t+2). За такой период постоянная составляющая прироста равна 2m, а ошибка равна сумме ошибок интервалов (t, t+1) и (t+1, t+2) , т. е. (e2t+e2t+1).

Оценки s12  и s22 дисперсии sy2  являются случайными величинами, подчиненными нормальному закону распределения (см. приложение 2 к главе VII). При этом

Таким образом, из выражений (7.57) и (7.58) следует, что дисперсия оценки s22  оказывается в два раза больше, чем дисперсия оценки s12. Здесь учтено, что при оценке s12 число степеней свободы равно 2Т, а при оценке s22  число степеней свободы равно Т.

Заметим, что в соответствии с (7.52), отношение  s22/s12 представляет собой случайную величину VR (2), определенную выражением (7.53). Это следует из того, что D(yt+yt–1)=s22, а D(yt)=s12. Иными словами,

VR (2)= s22/s12.                                   (7.59)

Используем формулу Тейлора для оценки сначала математического ожидания отношения VR (2). Получим (см. выражение (7.199) приложения 3 к главе VII)

M=1.                                   (7.60)

Далее согласно этой же формулы найдем дисперсию переменной (VR (2)–1)=, которая, как  показано в этом же приложении, определяется выражением

D=,                                   (7.61)

где, напоминаем, в данном случае 2Т – количество степеней свободы процесса yt, t=0,1,2,...,2Т  .

Таким образом, в случае справедливости ГСБ отношение  VR (2) при Т®¥  распределено приблизительно по нормальному закону, т. е.           (VR (2)–1)~, откуда в свою очередь следует, что

Результат (7.62) совпадает с рассмотренным выше интуитивным предположением.

Из выражения (7.62) непосредственно вытекает, что справедливость ГСБ может быть подтверждена или отвергнута на основании сопоставления расчетного значения  с пределами интегрирования стандартизованной плотности нормального распределения при заданной доверительной вероятности р*   и значении  Т+1 – числе измерений временного ряда yt, t=0,1,2,..., Т.

Иными словами, ГСБ принимается, если удовлетворяется соотношение

где х1    и х2   находятся из выражения

р(х1 £z£ х2)=р*=ò

и х1=–х2,

В частности, при р*=0,95 ГСБ справедлива, если интервал (7.63) имеет следующие пределы: х1 =–1,96, х2 =1,96. 

Рассмотренный тест несложно преобразовать для случая 2-го, 3-го и т. д. коэффициентов автокорреляции приростов ряда yt  и, следовательно, отношений VR (3), VR (4),... .

В частности, отношение VR (3), на основании которого может быть проверена гипотеза о равенстве нулю 2-го коэффициента автокорреляции ряда приростов процесса yt, формируется следующим образом:

где, в свою очередь, числитель s32   определяется следующим выражением:

Остальные характеристики, т. е. m  и s12, определены как и раньше выражениями (7.54) и (7.55) соответственно.

Как и в случае VR (2) можно показать, что случайная величина распределена при Т ®¥  по нормальному закону с параметрами (0,4).

В общем случае, случайная величина имеет также асимптотически нормальное распределение N(0,2(n–1)). Гипотеза о справедливости ГСБ в данном случае подтверждается с вероятностью р*, если расчетное значение VR (п) удовлетворяет соотношению (7.63) при случайной величине z, определяемой следующим выражением:

Таким образом, рассмотренные тесты позволяют проверить справедливость основной предпосылки всех версий ГСБ – отсутствие автокорреляционных связей в ряду приростов финансового показателя yt, t=1,2,..., Т; yt=lnYt.  Однако подтверждение этого предположения еще не указывает на конкретную версию ГСБ. Напомним, что различные версии ГСБ отличаются друг от друга либо наличием определенных закономерностей в рядах   функциональных преобразований этих приростов (ошибок), либо особыми свойствами дисперсии ошибки (гетероскедастичность). В частности, напомним, что ГСБ-1 и ГСБ-2 предполагают  полное отсутствие корреляционных связей между временными рядами квадратов значений ошибки (а также их третьих, четвертых степеней и т. п.). ГСБ-2 допускает некоррелированные изменения дисперсии этого процесса в рассматриваемом интервале, а ГСБ-3 допускает существование корреляционных взаимосвязей во временных рядах значений ошибки, возведенных во вторую, третью и т. д. степени, различных комбинаций рядов, полученных в виде произведений разновременных значений ошибки, т. е. типа et×et–i   и et×et–j  и т. п.

Таким образом, при справедливости ГСБ-1 дополнительно к условиям типа cov(et, et–i)=0, i=1,2,... должны выполняться условия, свидетельствующие об отсутствии автокорреляционных связей в рядах квадратов ошибки, ее произведений четвертого порядка и т. д. , что эквивалентно следующим соотношениям:

где et=(уt–уt–1–m).

При нарушениях условия (7.67) рассматриваемый процесс удовлетворяет условиям ГСБ-3.

В этом случае для проверки соответствия свойств рассматриваемого процесса предпосылкам ГСБ-1 или ГСБ-3 тестированию должны быть подвергнуты также временные ряды квадратов ошибки и их разновременных произведений. При этом могут использоваться те же самые тесты, которые были рассмотрены в разделе 7.3.

Справедливость предпосылок ГСБ-2 обычно устанавливается путем проверки условия постоянства дисперсии приростов в ряду рассматриваемого финансового показателя. Если условие

на интервале t=1,2,..., Т не выполняется, процесс удовлетворяет предпосылкам ГСБ-2. В случае выполнения этого условия рассматриваемый процесс удовлетворяет условиям ГСБ-1 (разумеется при выполнении также условия (7.67)). Для проверки условия (7.68) можно использовать тесты, основанные на критериях Фишера, Кокрена, Сиджела-Тьюки и другие, описанные в главе VI.

Заметим, что рассмотренные в данном разделе тесты обычно используются в исследованиях свойств временных рядов финансовых показателей с глубиной интервала наблюдений, не превышающей 1-2 года. В последнее время в научной литературе вырос интерес к исследованиям свойств временных рядов со значительно более обширной предысторией, охватывающей 10-летний и более продолжительные периоды. На таких интервалах в целом трудно ожидать выполнения предпосылок ГСБ-1. Однако и их нарушение можно обнаружить, лишь сопоставляя свойства процессов на различных достаточно больших временных промежутках, поскольку в период из 100-500 наблюдений такие процессы часто обладают свойствами строгого белого шума.

  Проверка таких свойств (соответствие предпосылкам ГСБ-1 на относительно коротких временных интервалах и соответствие ГСБ-2 или ГСБ-3 на длинных интервалах) осуществляется с использованием специального класса тестов (тесты сверхдлинных временных серий), рассмотрение которых выходит за рамки данного раздела.