Методы оценки параметров модели с изменяющейся вариацией

В общем случае определение параметров оценок моделей с изменяющейся вариацией является более сложной проблемой, чем оценка параметров моделей с постоянной вариацией. Дело в том, что эффекты, обусловленные взаимосвязями между квадратами ошибок, приводят к тому, что соотношения между параметрами модели и исходными данными становятся нелинейными и гораздо более сложными, чем в случае традиционных линейных эконометрических моделей. В такой ситуации в аналитическом виде получить решение становится невозможным, и поэтому обычно приходится прибегать к численным методам определения оценок, основанным на итеративных процедурах последовательного приближения.

Вместе с тем, общий подход для формирования уравнений, связывающих значения параметров моделей с изменяющейся вариацией с исходными данными, использует те же принципы, что и в случае моделей с постоянной вариацией. Он также обычно базируется на принципах максимального правдоподобия и минимума суммы квадратов ошибки.

Например, функция максимального правдоподобия для модели с изменяющейся вариацией в общем случае может быть записана в следующем виде:

при ограничениях, определяющих: а) особенности взаимосвязи между значениями процесса уt  и его условным математических ожиданием. Например,

б) особенности взаимосвязи между условными вариациями. Например, в случае GARCH-модели – это:

где, в свою очередь, значение ошибки et  является разностью между фактическим значением процесса в момент t – уt  и его условным математическим ожиданием mt:

В результате логарифм выражения (7.153), определяемый как

является функцией как параметров модели (7.154), которые в (7.157) скрыты под обозначением mt, так и параметров уt, являющихся исходными данными, как это было и раньше в случае линейных моделей с постоянной вариацией. Но, кроме этого, его значение в нашем случае также зависит от параметров ai  и bj, определяющих взаимосвязи между условными вариациями, i=1,2,..., k; j=1,2,..., r.

В результате система уравнений, на основе которой должны быть определены “оптимальные” значения параметров модели с изменяющейся вариацией, должна быть определена на основании дифференцирования правой части выражения (7.157) по параметрам векторов g=(g0,..., gп), a=(a0,..., ak) и b=(b1,..., br) и приравнивания к нулю соответствующих производных:

¶lnL/¶g=0;

¶lnL/¶a=0;

¶lnL/¶b=0.                                (7.158)

При этом получение самих дифференциалов осложняется наличием взаимосвязей между разновременными значениями vt и et, что, в свою очередь, значительно усложняет форму уравнений системы (7.158). В результате ее решения, т. е. оптимальные оценки параметров векторов g, a и b могут быть, как это отмечалось выше, определены лишь с помощью достаточно сложных численных методов решения.

Вместе с тем, для некоторых типов представленных здесь моделей методы оценки их параметров могут быть несколько упрощены на основе учета специфических свойств, описываемых ими процессов.

Рассмотрим основные подходы к оценке параметров моделей с изменяющейся вариацией на примере моделей (7.122) и (7.141).

Здесь сразу следует отметить, что в том случае, когда условная вариация vt  представляется как функция прошедших значений цен Yt–i, i=1,2,..., то исходная информация для получения оценок соответствующих моделей может быть сформирована, например, в виде ряда значений  st–i=(Yt–i–mt–i)2, где условное математическое ожидание mt–i определяется на основании модели, описывающей динамику цен, т. е. временного ряда Yt, t=1,2,..., Т.

В моделях типа (7.120) непосредственно сформировать значения vt, t=1,2,... не представляется возможным. Вследствие этого параметры соответствующих моделей могут быть получены опосредованно, например, с использованием значений процессов st  и zt .

Обозначим, как и в разделе 7.5, st=(Yt–m)2. Тогда выражение (7.123) можно переписать в следующем виде:

M=a0+ a1st–1,                              (7.159)

где M  означает условное математическое ожидание переменной st  при известном значении st–1 .

Напомним, что для уравнения авторегрессии первого порядка условное математическое ожидание         M=a0+a1xt–1  определяется точно также, как и для переменной st. Эквивалентность выражения (7.128) и ассоциированного с ним уравнения авторегрессии первого порядка позволяет непосредственно установить некоторые свойства процесса (7.123), которые могут быть использованы при получении приблизительных оценок параметров a0 и a1. В частности, при условии, что дисперсия переменной существует, в соответствии с выражением (6.58) имеем

где r1   (st)– первый коэффициент автокорреляции ряда st .

Переходя к безусловному математическому ожиданию переменной st , на основе выражения (7.159) получим

откуда непосредственно вытекает, что параметр a0 находится из соотношения

где

Заметим, что аналогичные рассуждения справедливы и в отношении более общей модели (7.121). Ее коэффициенты приблизительно могут быть оценены на основании системы Юла-Уокера (см. выражение (6.50)) для ряда st, а коэффициент a0 найден из соотношения:

Найденные оценки далее могут быть уточнены на основе  использования ММП. Заметим, что в общем случае оценке подлежат следующие параметры:  m, a0, a1,..., ak.  Функция правдоподобия в предположении, что ошибка распределена по нормальному закону может быть представлена в следующем виде:

Lk   (a ,  ) =  a ,  ),       (7.163)

где a=(a0, a1,..., ak) – вектор оценок параметров;   – оценка математического ожидания;

 a ,   ) =

и It–1={Y1, Y2,..., Yt–1}.

Натуральный логарифм функции (7.163) равен

ln Lk   (a , ) =     (7.165)

Максимизируя выражение (7.165) по параметрам , a0, a1,..., ak   при условии, что

получим систему нелинейных уравнений, выражающих эти параметры через значения процесса Yt. Далее, решая эти уравнения, найдем искомые значения , a0, a1,..., ak.

В моделях типа (7.120) сформировать значения ряда vt, t=1,2,..., Т, необходимые для оценки коэффициентов моделей с изменяющейся зависимой вариацией, непосредственно не представляется возможным. В такой ситуации иногда удается решить эту проблему, используя данные рядов st  и zt. Рассмотрим особенности оценки параметров уравнения типа (7.120) на примере модели (7.141). Заметим, что эта модель имеет три неизвестные параметра: a, b  – параметры закона распределения переменной ln(vt), a1 – параметр уравнения (7.141). Для нахождения этих параметров отметим основные соотношения, связывающие моменты процессов vt, zt  и st.

Для начала заметим, что в соответствии с выражением (7.132) мы имеем где

Далее  – дисперсия процесса vt.

Используя значения исходного ряда данных цен Yt, найдем оценки первых моментов для рядов zt  и st  на основании следующих выражений:

С учетом найденных значений несложно определить оценки математического ожидания и дисперсии процесса vt.

Для определения оценок параметров распределения случайной переменной lnvt   a и b используем известные  выражения для математического ожидания и второго начального момента переменной vt  (см.(7.137)): С учетом этого, дисперсию b2 переменной  lnvt   получим на основании следующего выражения:

Подставляя в (7.167) вместо моментов mv, sv2  их оценки из (7.166), получим следующую формулу для определения дисперсии b2  через  параметры распределения процессов zt  и st:

Аналогично, учитывая, что  получим формулу для  определения  значения его оценки в следующем виде:

Для определения параметра модели a1  (7.141) можно воспользоваться следующей процедурой сформированной с учетом известного выражения для параметра процесса  АР(1):  Отсюда, с использованием, например, выражения (7.144) получим:

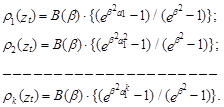
Обозначим через gi =   следующее выражение:

Тогда при известных значениях ri (zt) и b   значение оценки параметра a1  может быть найдено путем минимизации следующей квадратической функции:

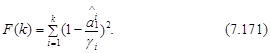
Выражение (7.171) представляет собой сумму квадратов отклонений отношений /gi   от единицы. Заметим, что, вообще говоря, значение a1=g1, а g1  является функцией от r1(zt ). Однако определение значения a1 только по одному значению коэффициента автокорреляции процесса zt может привести к значительной ошибке. Использование для этих целей ряда таких  коэффициентов способствует ее уменьшению.

Последующая процедура действий по восстановлению процесса vt   состоит в следующем. На основании найденных значений   и  с помощью модели (7.141) восстанавливается ряд натуральных логарифмов переменной vt   – ln(vt ).  При этом при определении lnv1   в качестве значения переменной v1 может быть использовано среднеквадратическое отклонение , где  –дисперсия переменной Yt.

Далее по ряду ln(vt) путем потенцирования находится переменная vt.

Найденная оценка коэффициента a1  может быть уточнена путем решения систем нелинейных уравнений, вытекающих из ММП, в котором она обычно используется в качестве начального приближения.

Предложенный метод оценки параметров авторегрессионных уравнений относительно ln(vt) несложно модифицировать и на модели более высоких порядков.