Пусть имеется множество, состоящее из N объектов. Каждый объект описывается с помощью n переменных (признаков, факторов). Совокупность значений переменных сведена в матрицу:
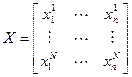, (10.1)
в которой наблюдения представлены в виде отклонений от выборочных средних, иначе говоря, центрированы, т.е. 
, 
,
где 
– среднее значение j-й переменной, 
– результат измерения j-го признака на i-м объекте.
От исходного вектора признаков 
перейдем к новому множеству переменных 
.
Каждую компоненту вектора z будем представлять в виде некоторой линейной комбинации исходных признаков, т.е. 
, j=1,2,…,n, (10.2)
где 
– вектор искомых весовых коэффициентов.
На компоненты вектора z наложим следующее требование: первая переменная 
должна быть ориентирована по направлению максимально возможной дисперсии, вторая − по направлению максимально возможной дисперсии в подпространстве, ортогональном первому направлению, и т.д. Компоненты вектора z, удовлетворяющие этому требованию, называют главными компонентами.
Поможем написать любую работу на аналогичную тему