Вычисление главных компонент

Вычисление весовых коэффициентов будем проводить последовательно, начиная с первой главной компоненты. Значение первой главной компоненты для i-го объекта  (i=1,2,…,N) составит .  (10.3)

Вводя векторное обозначение  , выражение (10.3) можно записать в виде .   (10.4)

Оценка дисперсии D(z1) центрированной переменной   есть по определению среднее квадрата ее значений. Таким образом,    .   (10.5)

  есть не что иное, как оценка матрицы ковариаций исходных признаков . Эту оценку обозначим . Выражение (10.5) примет вид:    .                                 (10.5а)

Вектор параметров  необходимо подобрать так, чтобы дисперсия D(z1) была максимальной. Если на параметры не накладывать никаких ограничений, то, очевидно, такая задача не имеет конечного решения. Потребуем, чтобы норма (длина) вектора , равнялась единице:   .                                         (10.6)

Для максимизации (10.5а) при ограничении (10.6) воспользуемся методом неопределенных множителей Лагранжа. Определим     ,

где  – множитель Лагранжа.

Дифференцирование  по отдельным элементам вектора  компактно может быть записано так:

. Полагая , получаем    .  (10.7)

Из (10.7) видно, что   – собственный вектор матрицы , соответствующий собственному значению λ1.

Из (10.6) и (10.7) следует, что  .

Поскольку  максимизируется, в качестве  выбирается наибольшее собственное значение матрицы .

При поиске значений элементов вектора , кроме ограничения на норму вектора, аналогичного (10.6), требуется обеспечить ортогональность векторов значений первой и второй главных компонент  и . Так как скалярное произведение ортогональных векторов равняется нулю, а матрица  симметричная и, следовательно, , то справедлива следующая цепочка равенств:

 .

Поскольку ни (N-1),  ни l нулю не равны, имеем:       .                                          (10.8)

Определим функцию Лагранжа следующим образом:  ,

где λ2  и  – множители Лагранжа.

Приравняем нулю частную производную φ по :    .

Умножая последнее равенство слева на  и принимая во внимание условие нормировки (10.6), получаем:   .

Учитывая, что  ,  а также условие (10.8), имеем:   .

Следовательно, соотношение (10.8) примет вид   ,

где в качестве   выбирается второе по величине собственное значение матрицы . Этот процесс продолжается до тех пор, пока не исчерпается список всех n собственных значений матрицы . Полученные в результате n собственных векторов матрицы составят ортогональную матрицу: .

В итоге, значения главных компонент задаются матрицей: .

Ковариационная матрица главных компонент есть .

Введем диагональную матрицу собственных значений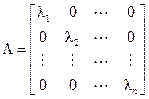      

Тогда , и окончательное выражение для ковариационной матрицы главных компонент приобретает вид     ,   поскольку  в силу ортогональности собственных векторов.

Следовательно, главные компоненты попарно некоррелированы, а их дисперсии совпадают с собственными значениями ковариационной матрицы исходных переменных.

Если ранг матрицы Х меньше n , то у матрицы  будет k нулевых собственных значений, и изменения в переменных  могут быть полностью выражены с помощью n-k  независимых переменных. При отсутствии нулевых собственных значений некоторые  могут оказаться весьма близкими к нулю, так что существенный вклад в суммарную дисперсию будут вносить первые несколько главных компонент.

Суммарная дисперсия исходных переменных, равная следу матрицы , равняется суммарной дисперсии главных компонент. Действительно,  .

Здесь мы воспользовались свойством неизменности следа произведения матриц при перестановке сомножителей, т.е. tr(AB)=tr(BA) (предполагается, что произведение ВА существует). Тогда отношения

,,…,,

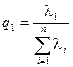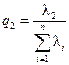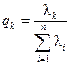характеризуют пропорциональный вклад каждого вектора, представляющего главные компоненты, в суммарную дисперсию исходных переменных.

Накопленные отношения  

показывают относительную долю в суммарной дисперсии исходных переменных, которая приходится на первые  k  главных компонент. Задавшись некоторым порогом , для дальнейшего анализа оставляют те первые k΄ главных компонент, для которых    .

В заключение сделаем два замечания.

1. Переход к главным компонентам наиболее естественен и эффективен, когда исходные признаки имеют общую физическую природу и измерены в одних и тех же единицах. Если это условие не имеет место, то результаты иcследования с помощью главных компонент будут существенно завиcеть от выбора масштаба и природы единиц измерения. В качестве практического средства в таких ситуациях можно рекомендовать переход к вспомогательным безразмерным признакам  нормированием исходных признаков  по формуле  где  – дисперсия i-го признака.

2. Аналитически доказано, что переход от исходного n-мерного пространства к m-мерному пространству главных компонент сопровождается наименьшими искажениями суммы квадратов расстояний между всевозможными парами точек наблюдений, расстояний от точек наблюдений до их общего центра тяжести, а также углов между прямыми, соединяющими всевозможные пары точек  наблюдений с их общим центром тяжести