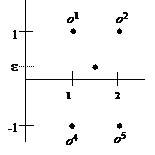Графическое представление результатов кластерного анализа.

Иерархическая классификация, как уже отмечалось, допускает наглядную интерпретацию. Для того чтобы привязать граф иерархии или дендрограмму к системе прямоугольных координат, введем понятие индексации. Индексацией h иерархии называется отображение h: h®R1, ставящее в соответствие множеству Kh число h (K)R1 таким образом, что

1)        h (K) = 0 для одноэлементных множеств K, т.е. ôKô = 1;

2)        h (K´) < h (K) для каждой пары (K´,K) такой, что K´K, K´≠  K.

Индексация иерархии позволяет алгоритмизировать процесс построения дендрограммы. Пусть (h,ν) – некоторая индексированная иерархия h на множестве О = {O1, O2, …,ON}. Вершины графа иерархии, отвечающие одноэлементным множествам {Oi}, i = 1,2, …, N, обозначим через νi, а вершины, соответствующие К (|К| > 1), обозначим νК. Введем систему координат с осью абсцисс х и осью ординат η. Вначале  на оси х через равные интервалы D размещаются вершины , то есть представляются в виде точек с координатами = (iD, 0). Предположим далее, что вершины и  уже нанесены на плоскость в виде точек с координатами  и . Тогда кластер K = KiKj может быть представлен точкой с координатами  с последующим соединением ее с точками  и . Напомним, что η К > max(,) согласно п.2 определения индексации, так что вершина vК расположится выше вершин  и . Заметим, что построенная таким образом дендрограмма может содержать нежелательные пересечения ребер, поэтому вершины переупорядочиваются так, чтобы ребра соединялись только в вершинах. На рис.9 представлены дендрограммы иерархии с пересечением и без. Заметим также, что традиционно ребра диаграммы изображают в виде вертикальных и горизонтальных отрезков, как на дендрограмме без пересечений (рис.9,б).

                              а)                                                                    б)

Рис.9. Дендрограммы иерархии примера из п.9.5.1:

а − с пересечением ребер; б − без пересечения ребер

Способы задания индекса ν могут быть разные. Весьма распространена индексация, ставящая в соответствие множеству Kh номер шага, на котором это множество было включено в иерархию. В качестве альтернативы индексом может выступать мощность множества, точнее ν = ôKô – 1.

Информативность дендрограммы существенно возрастает, если в качестве ординаты кластера K, полученного объединением кластеров Ki и Kj, т.е. K = KiKj, выступает расстояние между кластерами d(Ki, Kj). Такое изображение называют оцифрованным.

Одна из проблем иерархического кластерного анализа – определить, какие метрики позволяют провести оцифрование, удовлетворяющее условиям индексации, или иначе, найти индексацию, такую что ν(КiКj) = d(Кi,Кj). Так, для евклидовой метрики ответ на этот вопрос – отрицательный, что можно проиллюстрировать следующим примером. Пусть пять двумерных объектов, подлежащих кластеризации, образуют конфигурацию, представленную  на рис.10, а.

а)

б)

Рис.10. Пример инверсии для евклидовой метрики:

а − исходная конфигурация; б −  инверсия

На первом шаге агломеративной процедуры получаем кластер К1=.{О1, О2} c координатами центра тяжести Z(К1) = (1,5;1). Для кластера К1, полученного объединением одноэлементных кластеров {O1} и {O2}, d(О1, О2) = 1. Ближайшим к К1 окажется объект О3 (точнее одноэлементный кластер К2={O3}) с координатами центра тяжести v(К2)= (1,5; ). На следующем шаге алгоритма образуется, очевидно, кластер К3=К1К2 с d(К1, К2) = (1 – )2, поскольку расстояние между кластерами измеряется по центрам тяжести (квадрат евклидова расстояния). Выходит для кластера К3 потенциальный индекс, равный расстоянию (1–)2, оказывается меньше по сравнению с индексом К1, равным 1. Налицо инверсия, поскольку нарушено требование 2, предъявляемое к индексам: К1 К3 ® ν(К1) < ν(К3) (см. рис.10, б).

Достаточные условия, когда оцифрование является и индексацией, содержатся в теореме Миллигана. Эта теорема опирается на рекуррентную формулу Жамбю, которая позволяет пересчитывать расстояния между имеющимся кластером К и вновь образованным K¢=KiKj (K¹Ki, K¹Kj), используя расстояния и индексы, полученные на предыдущих шагах:  d(K, K¢) = a1d(K,Ki)+a2d(K,Kj)+a3d(Ki,Kj)+a4ν(K)+

+a5ν(Ki)+a6ν(Kj)+a7½d(K, Ki)–d(K,Kj)ú,

где ai – числовые коэффициенты, зависящие от метода определения расстояния между кластерами. Так, при

а1=а2=–а7=1/2 и а3=а4=а5=а6=0

приходим к расстоянию, измеренному по принципу «ближайшего соседа», а при

а1=а2=а7=1/2 и а3=а4=а5=а6=0   –  «дальнего соседа».

Теорема Миллигана. Пусть h – иерархия на О, полученная с использованием метрики d(К1,К2), для которой справедлива формула Жамбю. Тогда, если   а1+а2+а3³1, аj³ 0 для j=1,2,4,5,6  и  а7³–min (а1,а2),

то отображение h, задаваемое формулой h(К1К2) = =d(К1,К2) и условием ν({Оi})=0, i=1,2, …,N, является индексацией.

В заключение отметим, что если рассечь дендрограмму горизонтальной линией на некотором уровне h*, получаем ряд непересекающихся кластеров, число которых равно количеству «перерезанных» линий (ребер) дендрограммы; состав кластера определяется терминальными вершинами, связанными с данным «перерезанным» ребром.