Рассмотрим один из известных алгоритмов неметрического многомерного шкалирования, предложенный Дж. Краскалом. Пусть ![]()
![]() – оценки координат, где i – номер точки; k – номер координаты;
– оценки координат, где i – номер точки; k – номер координаты; 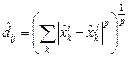 – оценка расстояний по
– оценка расстояний по ![]() -метрике;
-метрике; ![]() – ранговые образы расстояний, иначе отклонения. Эти величины должны соответствовать, насколько это возможно, оценкам расстояний, но с сохранением условия монотонности:
– ранговые образы расстояний, иначе отклонения. Эти величины должны соответствовать, насколько это возможно, оценкам расстояний, но с сохранением условия монотонности: ![]() . (12.1)
. (12.1)
Для оценки степени расхождения вводят меру соответствия (S-стресс):
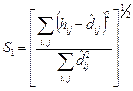 либо
либо 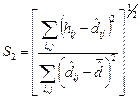 , где
, где ![]() – среднее арифметическое оцененных расстояний.
– среднее арифметическое оцененных расстояний.
Наряду с S-стрессом используется SS-стресс, где в числителе оценки расстояний и отклонения заменены их квадратами. SS-стресс обеспечивает более быструю сходимость, если матрица различий симметрична.
Алгоритм Краскала состоит из пяти основных этапов:
1) формирование стартовой конфигурации, то есть получение начальных оценок координат (размерность пространства предполагается известной);
2) стандартизация расстояний и оценок координат;
3) неметрический этап, в ходе которого вычисляются отклонения;
4) метрический этап: перерасчет оценок координат;
5) подсчет меры соответствия.
Если мера улучшилась, то возвращаются к этапу 2; в противном случае работа алгоритма завершается.
Рассмотрим перечисленные этапы подробнее. Стартовая конфигурация строится по методу Торгерсона (ортогональное проектирование). Затем по координатам найденных точек вычисляется матрица расстояний с элементами ![]() .
.
На втором этапе в ходе первой итерации текущие расстояния и координаты – те, которые получены из стартовой конфигурации. Для всех итераций, кроме первой, в качестве текущего расстояния и оценок используются те, что были получены на метрическом этапе предыдущей итерации.
Стандартизация оценок расстояний и координат состоит в делении их на сумму квадратов ![]() . Очевидно, подобное преобразование делает сумму квадратов расстояний равной единице, что снижает вероятность получения вырожденного решения и упрощает вычисления, особенно при использовании S1-стресса, выражение для которого приобретает вид
. Очевидно, подобное преобразование делает сумму квадратов расстояний равной единице, что снижает вероятность получения вырожденного решения и упрощает вычисления, особенно при использовании S1-стресса, выражение для которого приобретает вид 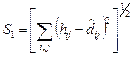 . (12.2)
. (12.2)
Поможем написать любую работу на аналогичную тему

