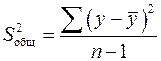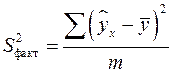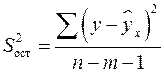После того как найдено уравнение регрессии, производиться оценка значимости уравнения в целом и его отдельных параметров.
Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. фактор ![]() не оказывает влияние на результат
не оказывает влияние на результат ![]() .
.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Общая сумма квадратов отклонений переменной ![]() от среднего значения
от среднего значения ![]() разлагается на две части – «объясненную» и «необъясненную»:
разлагается на две части – «объясненную» и «необъясненную»:
![]()
Т. е. общая сумма квадратов отклонений равна сумма квадратов отклонений (объясненная регрессия) плюс остаточная сумма квадратов отклонений.
Общая сумма квадратов отклонений индивидуальных значений результативного признака ![]() от среднего значения
от среднего значения ![]() вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый признак
вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый признак ![]() и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси
и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ![]() и
и ![]() . Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если прочие факторы не влияют на результат, то
. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной. Если прочие факторы не влияют на результат, то ![]() связан с
связан с ![]() функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора ![]() , т. е. регрессией
, т. е. регрессией ![]() по
по ![]() , так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того какая часть общей вариации признака
, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того какая часть общей вариации признака ![]() приходиться на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор
приходиться на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор ![]() оказывает существенное воздействие на результат
оказывает существенное воздействие на результат ![]() . Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 (![]() – число наблюдений,
– число наблюдений, ![]() – число параметров при переменной
– число параметров при переменной ![]() ).
).
Таблица 1.1
|
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Дисперсия на одну степень свободы |
|
Общая |
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
|
|
Факторная |
|
|
|
|
Остаточная |
|
|
|
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину ![]() -критерия Фишера:
-критерия Фишера:
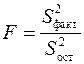 .
.
Фактическое значение ![]() -критерия Фишера сравнивается с табличным значением
-критерия Фишера сравнивается с табличным значением ![]() при уровне значимости
при уровне значимости ![]() и степенях свободы
и степенях свободы ![]() и
и ![]() . При этом, если фактическое значение
. При этом, если фактическое значение ![]() -критерия больше табличного, то признается статистическая значимость уравнения в целом.
-критерия больше табличного, то признается статистическая значимость уравнения в целом.
Для парной линейной регрессии ![]() , поэтому
, поэтому
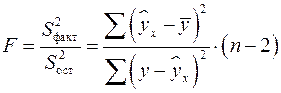 .
.
Величина ![]() -критерия связана с коэффициентом детерминации
-критерия связана с коэффициентом детерминации ![]() , и ее можно рассчитать по следующей формуле:
, и ее можно рассчитать по следующей формуле:
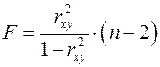 .
.
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: ![]() и
и ![]() .
.
Стандартная ошибка коэффициента регрессии определяется по формуле:
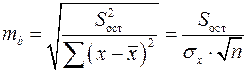 ,
,
где 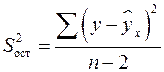 – остаточная дисперсия на одну степень свободы.
– остаточная дисперсия на одну степень свободы.
Величина стандартной ошибки совместно с ![]() -распределением Стьюдента при
-распределением Стьюдента при ![]() степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение ![]() -критерия Стьюдента:
-критерия Стьюдента: 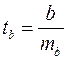 которое затем сравнивается с табличным значением при определенном уровне значимости
которое затем сравнивается с табличным значением при определенном уровне значимости ![]() и числе степеней свободы
и числе степеней свободы ![]() . Доверительный интервал для коэффициента регрессии определяется как
. Доверительный интервал для коэффициента регрессии определяется как ![]() . Поскольку знак коэффициента регрессии указывает на рост результативного признака
. Поскольку знак коэффициента регрессии указывает на рост результативного признака ![]() при увеличении признака-фактора
при увеличении признака-фактора ![]() (
(![]() ), уменьшение результативного признака при увеличении признака-фактора (
), уменьшение результативного признака при увеличении признака-фактора (![]() ) или его независимость от независимой переменной (
) или его независимость от независимой переменной (![]() ) (см. рис. 1), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например,
) (см. рис. 1), то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, ![]() . Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
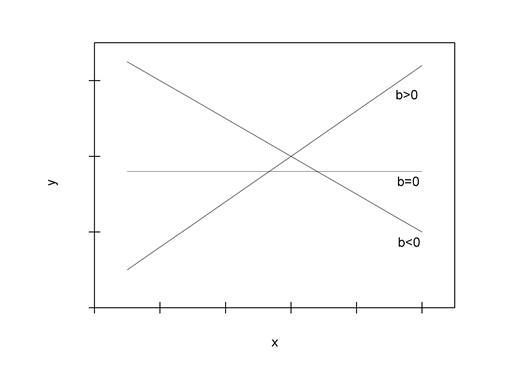
Рис. 1. Наклон линии регрессии в зависимости от значения параметра ![]() .
.
Стандартная ошибка параметра ![]() определяется по формуле:
определяется по формуле:
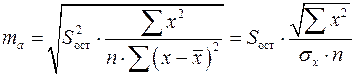 .
.
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии. Вычисляется ![]() -критерий:
-критерий: 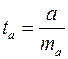 , его величина сравнивается с табличным значением при
, его величина сравнивается с табличным значением при ![]() степенях свободы.
степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции ![]() :
:
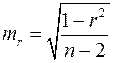 .
.
Фактическое значение ![]() -критерия Стьюдента определяется как
-критерия Стьюдента определяется как 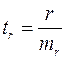 .
.
Существует связь между ![]() -критерием Стьюдента и
-критерием Стьюдента и ![]() -критерием Фишера:
-критерием Фишера:
![]() .
.
В прогнозных расчетах по уравнению регрессии определяется предсказываемое ![]() значение как точечный прогноз
значение как точечный прогноз ![]() при
при ![]() , т.е. путем подстановки в уравнение регрессии
, т.е. путем подстановки в уравнение регрессии ![]() соответствующего значения
соответствующего значения ![]() . Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки
. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ![]() , т.е.
, т.е. ![]() , и соответственно интервальной оценкой прогнозного значения
, и соответственно интервальной оценкой прогнозного значения ![]() :
:
![]() ,
,
где ![]() , а
, а ![]() – средняя ошибка прогнозируемого индивидуального значения:
– средняя ошибка прогнозируемого индивидуального значения:
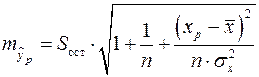 .
.
Поможем написать любую работу на аналогичную тему