Задача 1 - Задачи и ответы на контрольные вопросы по дисциплине Эконометрика.

По территориям региона за некоторый год приводятся данные о среднедушевом прожиточном минимуме в день на одного трудоспособного жителя страны (региона) в рублях, обозначаемые х, и среднедневная заработная плата в рублях — у. Соответственно: х — 78, 82, 87, 79, 89, 106, 67, 88, 73, 87, 76, 115; у — 133, 148, 134, 154, 162, 195, 139, 158, 152, 162, 159, 173.

1. Построить линейное уравнение парной регрессии у от х.

2.                 Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3.                 Оценить статистическую значимость параметров регрессии и корреляции и самого уравнения регрессии в целом.

Решение:

1.                 Для расчета параметров уравнения регрессии строим расчетную таблицу

;

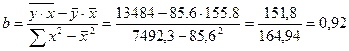 - уравнение регрессии.

2.  - линейный коэффициент парной корреляции;

, это означает, что 52% вариации заработной платы () объясняется вариацией фактора  - среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации: . Качество построенной модели оценивается как хорошее, так как  не превышает 8 – 10%.

3. Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей.

Выдвигаем гипотезу  о статистически незначимом отличии показателей от нуля: .

 для числа степеней свободы  и

Определим случайные ошибки , , :

; ;

.

Тогда ; ; .

Фактические значения t-статистики превосходят табличные значения:

;

;

, поэтому гипотеза  отклоняется, то есть ,  и  не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для   и .  Для этого определим предельную ошибку для каждого показателя:

, .

Доверительные интервалы:

; ;  ;

; ; .

С вероятностью  параметр  находиться в интервале , а параметр . Параметры не принимают нулевых интервалов, т. е. не являются статистически незначимыми и существенно отличны от нуля.