Оцените следующую структурную модель на идентификацию:
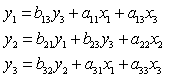 .
.
По приведенной форме модели уравнений:
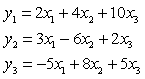
найдите структурные коэффициенты модели.
Решение:
Модель имеет три эндогенные ![]() и три экзогенные
и три экзогенные ![]() переменные. Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
переменные. Проверим каждое уравнение системы на необходимое (Н) и достаточное (Д) условия идентификации.
Первое уравнение
Н: эндогенных переменных – 2 ![]() , отсутствующих экзогенных – 1
, отсутствующих экзогенных – 1 ![]() .
.
Выполняется необходимое равенство: 2=1+1, следовательно, уравнение точно идентифицируемо.
Д: в первом уравнении отсутствуют ![]() и
и ![]() . Построим матрицу из коэффициентов при них в других уравнениях системы:
. Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение |
Отсутствующие переменные |
|
|
|
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
|
|
|
второе |
-1 |
|
|
третье |
|
0 |
![]() .
.
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется достаточное условие идентификации, значит, первое уравнение точно идентифицируемо.
Второе уравнение
Н: эндогенных переменных – 3 (![]() , отсутствующих экзогенных – 2
, отсутствующих экзогенных – 2 ![]() .
.
Выполняется необходимое равенство: 3=1+2, следовательно, уравнение точно идентифицируемо.
Д: во втором уравнении отсутствуют ![]() и
и ![]() . Построим матрицу из коэффициентов при них в других уравнениях системы:
. Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение |
Отсутствующие переменные |
|
|
|
|
|
|
первое |
|
|
|
третье |
|
|
![]()
Определитель матрицы не равен нулю, ранг матрицы равен2, следовательно, выполняется достаточное условие идентификации, второе уравнение точно идентифицируемо.
Третье уравнение
Н: эндогенных переменных - 2 ![]() , экзогенных отсутствующих – 1
, экзогенных отсутствующих – 1 ![]() .
.
2=1+1 – верно, следовательно, уравнение точно идентифицируемо.
Д: в третьем уравнении отсутствуют ![]() и
и ![]() . Построим матрицу из коэффициентов при них в других уравнениях системы:
. Построим матрицу из коэффициентов при них в других уравнениях системы:
|
Уравнение |
Отсутствующие переменные |
|
|
|
|
|
|
первое |
-1 |
0 |
|
второе |
|
|
![]()
Определитель матрицы не равен 0, ранг матрицы равен 2, следовательно, выполняется и третье уравнение точно идентифицируемо.
Следовательно, исследуемая система точно идентифицируема и может быть решена методом наименьших квадратов.
Вычислим структурные коэффициенты модели:
1) из третьего уравнения структурной формы выразим ![]() (так как его нет в первом уравнении структурной формы):
(так как его нет в первом уравнении структурной формы): ![]() . Данное выражение содержит переменные
. Данное выражение содержит переменные ![]() ,
, ![]() ,
, ![]() , которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение
, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение ![]() св первое уравнение приведенной формы модели (ПФМ):
св первое уравнение приведенной формы модели (ПФМ): ![]() , следовательно,
, следовательно, ![]() - первое уравнение СФМ.
- первое уравнение СФМ.
2) во втором уравнении СФМ нет переменных ![]() и
и ![]() . Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:
Первый этап: выразим ![]() из первого уравнения:
из первого уравнения: ![]()
Выразим ![]() из третьего уравнения ПФМ:
из третьего уравнения ПФМ: ![]() , подставим его в выражение для
, подставим его в выражение для ![]() :
: ![]() ;
;
![]() .
.
Второй этап: чтобы выразить ![]() , через искомые переменные
, через искомые переменные ![]() ,
, ![]() и
и ![]() подставим в выражение для
подставим в выражение для ![]() полученное из первого уравнения ПФМ выражение для
полученное из первого уравнения ПФМ выражение для ![]() :
: ![]() , следовательно,
, следовательно, ![]() . Подставим полученные
. Подставим полученные ![]() ,
, ![]() во второе уравнение ПФМ:
во второе уравнение ПФМ: ![]() , следовательно,
, следовательно, ![]() - второе уравнение СФМ.
- второе уравнение СФМ.
Из второго уравнения ПФМ выразим ![]() , так как его нет в третьем уравнении СФМ:
, так как его нет в третьем уравнении СФМ: ![]() . Подставим полученное выражение в третье уравнение ПФМ:
. Подставим полученное выражение в третье уравнение ПФМ: ![]() , следовательно,
, следовательно,
![]() - третье уравнение СФМ.
- третье уравнение СФМ.
СФМ примет вид:
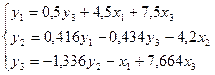
Поможем написать любую работу на аналогичную тему

