По 30 территориям России известны данные о среднедневном душевом доходе в рублях (у), среднедневной заработной плате одного работающего в рублях (x1 ) и среднем возрасте безработного (x2 ). Все данные представлены средними значениями, стандартными отклонениями и линейными коэффициентами парной корреляции соответственно для каждого признака: 86,8; 54,9 и 33,5 — средние отклонения; 11,44; 5,86 и 0,58 — стандартные. Наконец, линейные коэффициенты парной линейной корреляции: 0,8405 — у от x1 ; -0,2101 — у от x2 и -0,1160 — x1 от x2 .
1. Построить уравнение множественной регрессии в стандартизованной и естественной формах.
2. Рассчитать частные коэффициенты эластичности.
3. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
Рассчитать общий и частные F-критерии Фишера.
Решение:
1. Линейное уравнение множественной регрессии ![]() от
от ![]() и
и ![]() имеет вид:
имеет вид: ![]() . Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе:
. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе: ![]() .
.
Расчет ![]() -коэффициентов:
-коэффициентов:
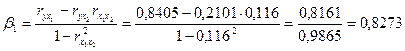
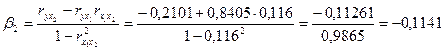 .
.
Получим ![]() - уравнение множественной регрессии в стандартизированной форме.
- уравнение множественной регрессии в стандартизированной форме.
Для получения уравнения в естественной форме рассчитаем ![]() и
и ![]() , используя формулы для перехода от
, используя формулы для перехода от ![]() к
к ![]() :
: ![]() ;
; 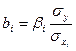 .
.
![]()
![]() .
.
Значение ![]() определим из соотношения
определим из соотношения ![]() ,
,
![]() - уравнение множественной регрессии в естественной форме.
- уравнение множественной регрессии в естественной форме.
2. Для характеристики относительной силы влияния ![]() и
и ![]() на
на ![]() рассчитаем средние коэффициенты эластичности:
рассчитаем средние коэффициенты эластичности: ![]() ;
;
![]() ;
; ![]()
3. Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
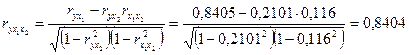 ;
;
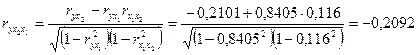 ;
;
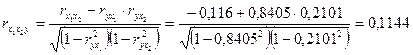 .
.
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (![]() ) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
![]() ,
, ![]() ;
; ![]() ;
;
![]() ,
, ![]() ;
; ![]() .
.
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов ![]() и
и ![]() :
:
![]() .
.
Зависимость ![]() от
от ![]() и
и ![]() характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации
характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации ![]() .
.
Общий F-критерий проверяет гипотезу ![]() о статистической значимости уравнения регрессии и показателя тесноты связи (
о статистической значимости уравнения регрессии и показателя тесноты связи (![]() ):
):
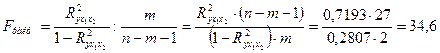 ;
;
![]() ,
, ![]() .
.
Сравнивая ![]() и
и ![]() , приходим к выводу о необходимости отклонить гипотезу
, приходим к выводу о необходимости отклонить гипотезу ![]() , так как
, так как ![]() . С вероятностью
. С вероятностью ![]() делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи
делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи ![]() , которые сформировались под неслучайным воздействием факторов
, которые сформировались под неслучайным воздействием факторов ![]() и
и ![]() .
.
Частные F-критерии - ![]() и
и ![]() оценивают статистическую значимость присутствия факторов
оценивают статистическую значимость присутствия факторов ![]() и
и ![]() в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т. е.
в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т. е. ![]() оценивает целесообразность включения в уравнение фактора
оценивает целесообразность включения в уравнение фактора ![]() после того, как в него был включен фактор
после того, как в него был включен фактор ![]() . Соответственно
. Соответственно ![]() указывает на целесообразность включения в модель фактора
указывает на целесообразность включения в модель фактора ![]() поле фактора
поле фактора ![]() :
: 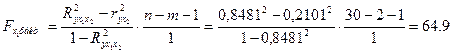 .
.
![]() ;
; ![]() .
.
Сравнивая ![]() и
и ![]() , приходим к выводу о целесообразности включения в модель фактора
, приходим к выводу о целесообразности включения в модель фактора ![]() после фактора
после фактора ![]() , так как
, так как ![]() . Гипотезу
. Гипотезу ![]() , о несущественности прироста
, о несущественности прироста ![]() за счет включения дополнительного фактора
за счет включения дополнительного фактора ![]() , отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора
, отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора ![]() после фактора
после фактора ![]() .
.
Целесообразность включения в модель фактора ![]() после фактора
после фактора ![]() проверяет
проверяет ![]() :
:
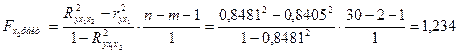
Низкое значение ![]() (немногим больше 1) свидетельствует о статистической незначимости прироста
(немногим больше 1) свидетельствует о статистической незначимости прироста ![]() за счет включения в модель фактора
за счет включения в модель фактора ![]() поле фактора
поле фактора ![]() . Следовательно, подтверждается нулевая гипотеза
. Следовательно, подтверждается нулевая гипотеза ![]() о нецелесообразности включения в модель фактора
о нецелесообразности включения в модель фактора ![]() (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, и нет необходимостиулучшать ее, включая дополнительный фактор
(средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, и нет необходимостиулучшать ее, включая дополнительный фактор ![]() (средний возраст безработного).
(средний возраст безработного).
Поможем написать любую работу на аналогичную тему

