Нагрузки как случайные величины.  Снеговые нагрузки

Для расчета сооружений на длительные сроки требуется значение максимальной снеговой нагрузки за много лет. Поскольку корреляция между годовыми нагрузками практически отсутствует, многолетнюю снеговую нагрузку можно получить теоретически, зная функцию распределения максимальной годовой нагрузки.

Обычно для описания максимальной годовой снеговой нагрузки используют законы распределения Гумбеля

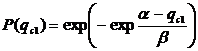                                                   (57.4),

хотя этот закон допускает вероятность отрицательных значений qc1.

Коэффициенты a и b имеют различные значения для разных местностей. Например, для Москвы a = 931 Н/м2, b = 365 Н/м2.

Для определения максимально допустимой снеговой нагрузки на сооружение, рассчитанное на n лет, вероятность непревышения его значения qcn:

                                                              (1.12).

Или вероятность превышения величины qcn за n лет

                                                               (2.12)

                                                             (3.12).

С помощью (3.12) величину qc1, соответствующую заданному числу лет n и допустимой вероятности Q легко определить графически по кривой интегрального закона распределения .

Подставляя (1.12) в (57.4) получим

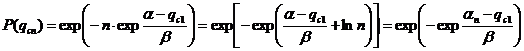        (4.12),

где .

Т.о., переход от максимума за год к максимуму за n лет (при распределении Гумбеля) приводит к поступательному смещению кривой P(qc1) вдоль ОХ вправо на величину . Также смещается и p(qc1).

Тогда можно записать

                                                               (5.12),

но дисперсия при этом не изменяется D(qcn)=D(qc1).

Если рассматривать снеговую нагрузку как случайный стационарный процесс, то его можно задать следующим образом:

Для г. Волгограда – аппроксимация функции м.о. высоты снегового покрова:

,

где h0 = 4,3 см – среднее значение;

А0 = 4,2 см – амплитуда;

Т = 180 дней – период математического ожидания.

Корреляционная функция случайного процесса h(t) аппроксимируется функцией

,

где D=D(h)=55,67 см2 – дисперсия высоты снегового покрова;

a = 0.04 день-1 – параметр функции.