Сочетания нагрузок как случайных величин

Если все нагрузки распределены по одному и тому же закону, то математическое ожидание их суммы:

; .

Коэффициент вариации (изменчивости) снижается при увеличении .

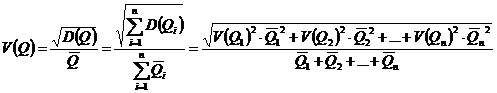,        (8.1)

где ;

,  — коэффициент вариации и математическое ожидание  точки случайной нагрузки .

Формулы справедливы для корреляционно не связанных нагрузок.

В случае, когда отдельные независимые нагрузки по-разному приложены к конструкции и усилие в рассчитываемом элементе (например, колонне) выражается линейной функцией , тогда коэффициент вариации случайного усилия :

,                     (8.2)

где 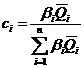.                                                                                                    (8.3)

Например, для колонны, если  — это распределенная нагрузка (кН/м2), то  — это грузовая площадь  нагрузки, м2.

Приведенный (средний) коэффициент перегрузки:

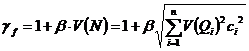,                                        (8.4)

где  — характеристика безопасности

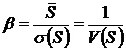,                                                    (8.5)

где  — случайная величина резерва прочности.

Расчетное усилие:

.                                 (8.6)

Приняв ,

где  — коэффициент перегрузки отдельных нагрузок,

получим общий коэффициент надежности по нагрузкам как случайную величину, выраженную через детерминированные значения частных коэффициентов надежности по А.Р. Ржаницыну:

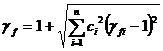;                                              (8.7)

если  

;

;

;

;

;

кПа;

, , , то

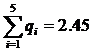кПа;

; ; ; ; ;

и общий коэффициент надежности по нагрузке:

;

кПа;

кПа;

Учет всех коэффициентов в отдельности дает 2.8525 кПа (). Таким образом, учет вероятностной природы нагрузок дает экономию по сравнению с расчетом по детерминированному подходу.