Фазовое пространство. Фазовая плотность вероятности

С макроскопической точки зрения состояние физической системы определяется небольшим числом измеримых параметров. Задание таких параметров определяет макроскопическое состояние системы.

Однако если повторить эксперимент, то микроскопические конфигурации атомов будут различны. Назовем состояние системы, Которое может быть полностью заданно  набором микроскопических переменных (координат и импульсов молекул) микроскопическими состоянием системы.

В классической физике микросостояние системы N частиц (бесструктурных) полностью задается 6N переменными (координаты и импульсы).

Сам процесс измерения подразумевает взаимодействие с макроскопическим прибором → даже если в системе 1 частица, она успеет побывать во многих микросостояниях. Поэтому, исходя из макроизмерений, можно делать только статистические (вероятностные)  суждения о значениях  микроскопических переменных.

Пусть над системой находящейся в определенном макросостоянии производится m наблюдений в следующие друг за другом моменты времени:

, .

При каждом наблюдении система оказывается в одном из своих допустимых микросостояний.

Если – число случаев, когда при наблюдении установлено, что система находилась в состоянии . Тогда вероятность обнаружения системы в микросостоянии :

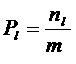 при .

Условие нормировки: .

Таким образом, с помощью длительного наблюдения за системой, находящейся в определенном макросостоянии, каждому допустимому микросостоянию  можно приписать определенный вес .

Данное распределение вероятности по допустимым микросостояниям однозначно соответствует некоторому макросостоянию и, наоборот, с точки зрения СФ каждое независимое макросостояние системы однозначно определяется распределением вероятности по ее допустимым микросостояниям – основной постулат СФ.

Так какизмерить микросостояние системы практически невозможно, то такое вероятностное описание оказывается наиболее полным.

Определение вероятности приводит к определению среднего значения физической величины, т.е. того значения, которое измеряется в макроэксперименте.

Пусть – значение величины в микросостоянии . Среднее значение тогда может быть вычислено по формуле из теории вероятностей:

.

Такое среднее является временным средним для одной системы. Однако в этом случае  может зависеть от времени.

Существует и другой подход (Больцман, Гиббс). Вместо временного усреднения в рамках одной системы было предложено в определенный момент времени рассматривать совокупность большого числа систем, устроенных так же как реальная система.

Среднее значение в определенный момент времени определяется по этой совокупности систем, а сама совокупность называется ансамблем систем. Такое среднее называется средним по ансамблю. Каждая система из ансамбля является точной копией реальной системы в одном из ее допустимых микросостояний. При этом макросостояние остается фиксированным, а систем в ансамбле должно быть столько же, сколько найдется микросостояний.

Доказательство эквивалентности средних по ансамблю и временных средних представляет собой сложную задачу, которая до сих пор в общем случае не решена. Это так называемая эргодическая проблема.

Основное предположение СФ состоит в том, что любая система из замкнутого ансамбля столь же хороша (столь же вероятна) как и любая другая система.

Таким образом, принцип априорных равных вероятностей годится для замкнутых систем и устанавливает равновероятность всех микросостояний в системе. Принцип не работает для части системы или для незамкнутой системы.

Этот постулат необходим для построения статистической физики. Справедливость его подтверждена следствиями, согласующимися с экспериментом. Речь идет о средних значениях, но всегда есть флуктуации.

В замкнутой системе выполняются законы сохранения. Однако, каждому значению сохраняющейся макровеличины (например, энергии) может соответствовать несколько конфигураций атомов. Они равновероятны.

Классическое фазовое пространство

Классическое приближение является предельным случаем более точной кв. механики. К микрообъектам оно применимо далеко не всегда. В классической статистической физике отсутствует квантование состояний – частицы системы могут иметь любые координаты q и импульсы p, удовлетворяющих уравнениям движения Ньютона.

В классической механике одной из основных величин, которая определяет движение системы, является гамильтониан:

 – сумма кинетической и потенциальной энергий.

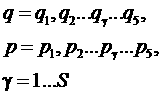
где qи p обобщенные координаты и импульсы

Уравнения движения Гамильтона имеют вид:

, , .

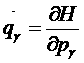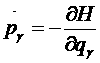При заданных начальных условиях  решение этих двух уравнений позволяет однозначно рассчитать эволюцию системы во времени: .

Воображаемое 2S мерное пространство, построенное из S координат и S сопряженных им импульсов, называется фазовым пространством (для одномерного движения одной частицы это будет фазовая плоскость).

Точка А в этом пространстве, заданная 2S числами, полностью определяет микроскопическое состояние системы в момент времени t. Совокупность точек (фазовый объем) определяет статистический ансамбль.

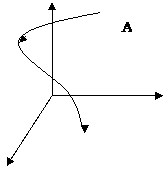
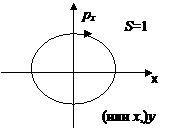Пример

При эволюции системы во времени изображающая ее точка движется по траектории в фазовом пространстве. Эту траекторию можно представить совокупностью 2S функций времени .

Элемент объема в классическом фазовом пространстве:

.

Фазовая плотность вероятности

Наблюдая поведение классической макросистемы можно определить вероятность того, что она будет обнаружена в некотором определенном микросостоянии. Пусть это микросостояние определяется малым элементом фазового объема , а процесс протекает за время от 0 до t. Пусть в течение времени  фазовая траектория проходит в пределах . Тогда вероятность  того, что система во время будет обнаружена в физическом состоянии , равна: .

Предел этого отношения при неограниченном увеличении времени наблюдения tопределяет вероятность того, что макросистема находится в определенном микросостоянии:

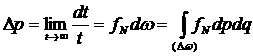, где функция  называется фазовой плотностью вероятности (функция распределения ансамбля систем) – размерная функция.

         Она удовлетворяет условию нормировки

,  .

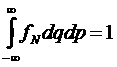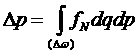         Тогда среднее значение некоторой динамической функции можно записать в виде

.

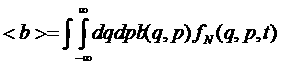Здесь интегрирование идет по всему фазовому пространству.