Энтропия – мера неопределенности при статистическом описании. Статистическое обоснование третьего начала термодинамики

Определение энтропии получено для– канонического распределения Гиббса. Для произвольной функции распределения  введем энтропию (опуская ):

 (квадратные скобки означают, чтовеличина определена для совокупности случайной величин Х),

.

Это для непрерывной переменной. Во многих случаях (в частности, в квантовой теории) используются функции распределения случайных величин, принимающих дискретный ряд значений n (например, набор квантовых чисел). Обозначим соответствующую функцию . Тогда: .

Тогда энтропия для дискретного распределения может быть представлена в виде

.

Свойства  и

1. Если  при , и нулю для всех остальных значений, то . Это соответствует нулевой неопределенности задания состояния системы.

2.     Если число возможных значений дискретной переменной  равно  и все возможные значения равновероятны: , , (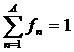–доказать).

То можно показать, что  в этом случае максимальна и равна:

.

В таком виде формула для энтропии была получена еще Больцманом.

 Это соответствует полному хаосу (максимальной неопределенности) задания состояния системы.

Для энтропии непрерывных величин  результаты аналогичны.

Для сравнения найдем энтропию, соответствующую квантовому микроканоническому распределению Гиббса:

.

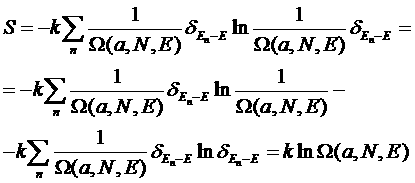Второе слагаемое равно нулю, поскольку содержит 0ln0 или 1ln1. Таким образом, мы снова получаем формулу для энтропии в виде:

.

Следовательно, энтропия может служить мерой неопределенности при статистическом описании процессов в макротелах.Такое определение энтропии можно использовать и для исследования неравновесных процессов, когда

.

Третье начало термодинамики с точки зрения статистической физики

На основе анализа экспериментов Вальтер Нернст (1906 г.) пришел к выводу, что разность энтропий  соответствующих любым двум модификациям вещества стремиться к нулю при приближении к нулю абсолютной температуры: .

Позднее Планк сформулировал Результат Нернста в еще более определенной форме:  при – теорема Нернста (третье начало).

Из нее следует ряд термодинамических следствий. Обратимся к квантовому каноническому распределению Гиббса. Из него следует выражение для энтропии:

.

Из квантового канонического распределения Гиббса следует, что наиболее вероятным является квантовое состояние системы с наименьшим возможным значением энергии – основное состояние.

В равновесном состоянии функция распределения  максимальна для основного состояния. Если через  обозначить разность энергий основного и возбужденного состояний, то при температуре  вероятность функции  для основного состояния будет близка к единице, а при Т=0: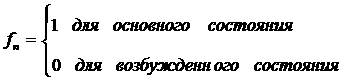

Эта функция удовлетворяет условию нормировки.

Действительно, записывая условие нормировки в виде:

,

получим

.

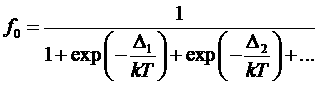При таком распределении все члены выражения для  равны нулю  при .

Таким образом, третье начало с точки зрения статистической физики можно сформулировать так:

при  система находится только в основном состоянии, поэтому неопределенность задания состояния равна нулю. Этому соответствует равенство нулю энтропии, которая является мерой неопределенности состояния при статистическом описании.