Обозначим через 
распределение, не совпадающее в общем случае с распределением Гиббса.
.
Кроме того, внутренняя энергия, вычисленная с помощью 
одинакова (
-неизменные).
.
В остальном 
-произвольная.
Обозначим через 
энтропии: 
, 
, и покажем, что 
. Т.е. энтропия, отвечающая каноническому распределению Гиббса, максимальна (равенство имеет место, если 
).
Представим 
в виде:
,
где 
-произвольная (вспомогательная) функция, определяемая . При этом должно выполняться условие нормировки:
.
Найдем разность энтропий:
.
Второй и четвертый члены, содержащие Н, сокращаются (вследствие одинаковости U). Тогда получим:
(*)
Здесь использовано условие нормировки
. Добавим к правой части (*) нулевой(опять из нормировки) член: 
.
Тогда получим
.
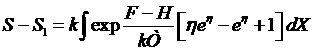Первый множитель под интегралом положителен, т.к. это экспонента.
Но второй множитель так же положителен:
. Легко показать, что он имеет минимум, равный нулю при 
.
Таким образом, получим: . Равенство имеет место, если .
Можно трактовать это и иначе: вместо можно выбрать 
, где 
- любой момент времени, отвечающий эволюции к равновесному состоянию. Тогда 
В замкнутой системе в ходе процесса эволюции к равновесному состоянию энтропия достигает максимального значения в равновесном состоянии. 
второй закон для необратимых процессов в замкнутой системе.
Как найти статистическая теория неравновесных процессов.
Поможем написать любую работу на аналогичную тему