Рассмотрим теперь идеальный квантовый газ, в котором нет взаимодействия между частицами. Рассмотрим пространство квантовых чисел K. Обозначим через ![]() число атомов, квантовые числа которых
число атомов, квантовые числа которых ![]() равны K, то есть:
равны K, то есть:
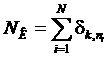 ,
, ![]()
где ![]() –случайная функция в пространстве квантовых чисел. Для системы с заданным числом частиц, находящейся в термостате, распределение
–случайная функция в пространстве квантовых чисел. Для системы с заданным числом частиц, находящейся в термостате, распределение ![]() определяется квантовым каноническим распределением Гиббса. Перепишем его в другом виде (используя
определяется квантовым каноническим распределением Гиббса. Перепишем его в другом виде (используя ![]() ). Для идеального газа энергия
). Для идеального газа энергия ![]() равна сумме энергий отдельных атомов:
равна сумме энергий отдельных атомов: 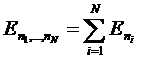 .
.
С другой стороны можно записать: 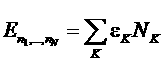 .
.
Переходя к потенциалу (большой термодинамический потенциал)![]() запишем распределение Гиббса в виде:
запишем распределение Гиббса в виде:
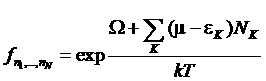 ,
, ![]()
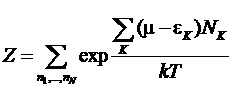 ;
; 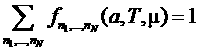 .
.
Z представим в виде: ![]()
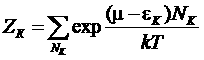 (*)
(*)
и перейдем к суммированию по Nk.
Соответственно:
![]() ,
, 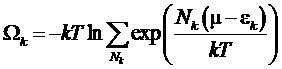 .
.
Тогда можно ввести функцию распределения по числам частиц на уровне k:
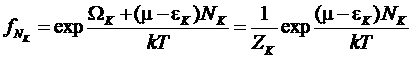 ,
,
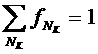 .
.
С помощью этой функции получим искомое выражение для ![]() – среднего числа частиц в квантовом состоянии К:
– среднего числа частиц в квантовом состоянии К:
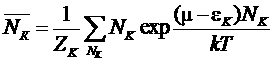 .
.
Используя определение ![]() , можно записать:
, можно записать:
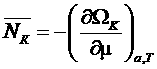 . (**)
. (**)
![]() – это условие позволяет установить при заданных
– это условие позволяет установить при заданных ![]() связь
связь ![]() с
с ![]() :
:
![]() .
.
Распределения Бозе и Ферми
Системы частиц с целым спином называются системами Бозе (статистика Бозе). Для таких систем числа заполнения ![]() состояний К могут быть произвольными:
состояний К могут быть произвольными:
![]() .
.
При этом условии сумма по ![]() в выражении для
в выражении для ![]() (*) представляет из себя геометрическую прогрессию, тогда:
(*) представляет из себя геометрическую прогрессию, тогда:
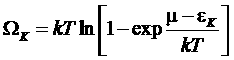 .
.
Дифференцируем по ![]() (**) и получим
(**) и получим
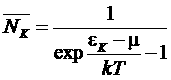 – распределение Бозе (Бозе – Эйнштейна).
– распределение Бозе (Бозе – Эйнштейна).
Такое распределение впервые было предложено Шатьендранатом Бозе для фотонов, Эйнштейн же обобщил его на произвольные системы частиц с целым спином.
Частицы с полуцелым спином удовлетворяют принципу Паули, согласно которому величина ![]() может принимать лишь два значения:
может принимать лишь два значения: ![]() .
.
В этом случае (*) примет вид
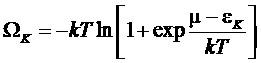 ,
,
тогда из (**) получим
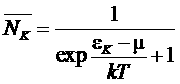 – распределение Ферми (Ферми – Дирака).
– распределение Ферми (Ферми – Дирака).
В случае, когда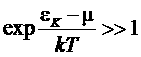 формулы Бозе и Ферми сводятся к одной
формулы Бозе и Ферми сводятся к одной
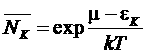 .
.
Это ни что иное, как распределение Больцмана.
Можно показать, что это неравенство соответствует другому:
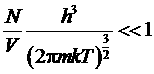 .
.
При выполнении этого неравенства газ называется невырожденным. В этом случае можно использовать распределения Максвелла и Больцмана. При выполнении обратного неравенства газ называется вырожденным и для его описания используются распределения Ферми и Бозе.
Поможем написать любую работу на аналогичную тему
Реферат
Распределение атомов идеального газа в пространстве квантовых состояний. Распределения Ферми и Бозе
От 250 руб
Контрольная работа
Распределение атомов идеального газа в пространстве квантовых состояний. Распределения Ферми и Бозе
От 250 руб
Курсовая работа
Распределение атомов идеального газа в пространстве квантовых состояний. Распределения Ферми и Бозе
От 700 руб

