Из опыта известно, что любой разряженный газ ведет себя как идеальный. Взаимодействие (в этом приближении) не учитывается. Член с потенциальной энергией в функции Гамильтона учитывает действие внешних полей (например, тяжести).
Пусть газ заключен в сосуд объема Vсо стенками, непроницаемыми для атомов. Наличие стенок можно учесть в функции Гамильтона путем введения потенциальной энергии следующего вида:
.
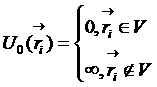Если такую потенциальную энергию подставить в канонического распределение Гиббса, то это приведет к тому, что если хотя бы один атом находился вне объема, то функция распределения равна нулю. Из термодинамики следует, что для нахождения уравнения состояния надо знать свободную энергию (а значит 
). Многомерный интеграл по переменным всех частиц сводится к произведению интегралов, поскольку все N
частиц равноправны:
, 
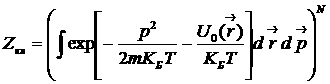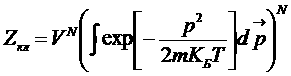
(указанный интеграл –интеграл Пуассона),
,
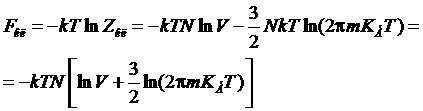
– свободная энергия классического газа.
Из термодинамики: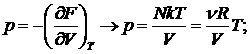 
–это уравнение состояния идеального газа, которое совпадает с экспериментальным.
Энтропия: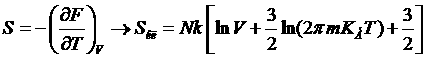 
.
Однако результаты для 
, 
не являются удовлетворительными т.к. в термодинамическом пределе (
, но
) они должны быть 
, поскольку эти величины аддитивные. Но у нас получается, что 
. Одним из следствий такого противоречия является Парадокс Гиббса.
Парадокс Гиббса
Пусть имеется сосуд, разделенный перегородкой на две равные части, каждые объема V. Число частиц в каждой части N. Обе половины наполнены одним и тем же газом. Если убрать перегородку, то физическое состояние системы останется неизменным. Естественно ожидать, что энтропия системы не изменится, поскольку нет никаких необратимых процессов в такой системе. Однако, расчет энтропии по классической формуле противоречит этому предположению.
При наличии перегородки: 
, где 
– вся, 
– одной половины (здесь использовано свойство аддитивности для энтропии).
После снятия перегородки:
.
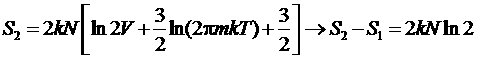Положительная разность энтропий означает, что при снятии перегородки энтропия системы возрастает! Для разных газов будет такое же изменение энтропии.
Для решения парадокса Гиббс предположил, что константа, с точностью до которой определяется энтропия 
зависит от N, причем так, что изменение энтропии после снятия перегородки будет равно нулю. Однако очевидно, что такое решение парадокса является искусственным, поскольку ниоткуда не следует, что константа должна иметь именно такой вид. Строгое решение парадокса оказалось возможным только в рамках квантовой статистической физики.
Поможем написать любую работу на аналогичную тему