Уравнение Лиувилля. Теорема Лиувилля

Рассмотрим поведение во времени фазового объема , соответствующего замкнутой системе.

Изменение  во времени происходит за счет изменения                                              координат и импульсов частиц.

В этом смысле движение изолированной системы в фазовом пространстве подобно потоку несжимаемой жидкости. Микросостояния не возникают и не исчезают, а изменяются в соответствии с законами механики.

Рассмотрим изменение во времени величины (эволюцию ансамбля). В начальный момент . Нужно предсказать .

Чисто формальным образом это передвижение фазовых точек можно рассматривать как стационарное течение «газа» в 2S-мерном фазовом пространстве и применять к нему известное уравнение непрерывности, выражающее собой неизменность массы (числа точек). Эта аналогия основана на том, что траектория точки не может закончиться или начаться вследствие однозначности уравнений механики.  То есть фазовые точки в изолированной системе не исчезают и не появляются.

Для газа таких точек можно записать уравнение непрерывности, которое представляет собой закон их сохранения:

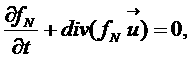
(–плотность, – скорость газа), а для стационарного течения

.

Обобщаяпоследнее уравнение на случай 2S-мерного пространства, получим

.

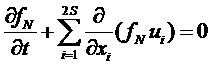В данном случае «координатами»  являются координаты qи импульсыp, а «скоростями» – производные по времени , определяемые уравнениями механики. Таким образом, имеем:

.                     (*)

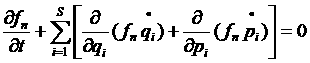Используя уравнения движения из классической механики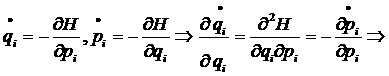получим, что уравнение может быть представлено в виде (при этом левая часть представляет собой полную производную по времени от функции распределения):

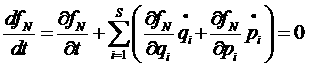– уравнение Лиувилля.

Следствием уравнения Лиувилля является сохранение фазового объема при движении системы (теорема Лиувилля). Однако форма объема при этом может меняться. Сохранение объема следует из факта сохранения числа фазовых точек в пространстве: микросостояния не исчезают и не появляются вследствие однозначности уравнений механики. Тогда можно записать:

Отсюда сразу следует сохранение элементарного объема.

Из теоремы Лиувилля следует, что функция распределения должна выражаться через такие комбинации p и q, которые с течением времени остаются постоянными. Это механические интегралы движения. Если отвлечься от поступательного и вращательного движений системы как целого, то функция распределения должна определяться энергией системы.

Математическим выражением сохранения фазового объема является равенство единице якобиана (смысл Якобиана как раз и состоит в отношении объемов при преобразовании координат):

.

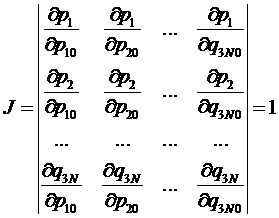Новые переменные связаны со старыми следующим образом:

.

Равенство модуля якобиана единице как раз и означает сохранение фазового объема.