Рассмотрим классическую систему, и покажем, что на каждую степень свободы в такой системе приходится энергия, равная kT/2. То есть, нам нужно доказать равенство:
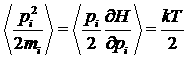 .
.
Используем каноническое распределение Гиббса:
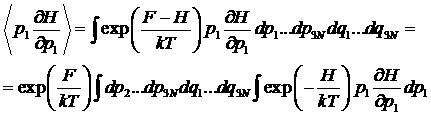 .
.
Интеграл по p1 можно взять по частям:
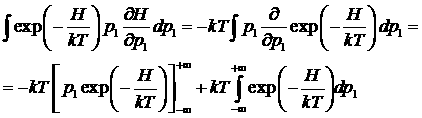 .
.
Слагаемое в квадратных скобках равно нулю, поскольку экспонента стремится к нулю быстрее, чем степенная функция. Поэтому
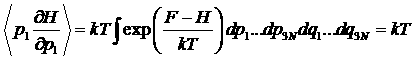 ,
,
поскольку интеграл в силу условия нормировки равен единице. Значение i=1 мы взяли произвольно. Такое же выражение можно получить для любого i.
Для координат можно получить аналогичное выражение:
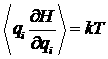 .
.
Важно только то, что при возрастании координат H тоже возрастает достаточно быстро. Например, для гармонического осциллятора имеем:
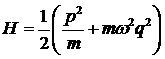 ,
, 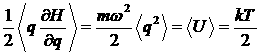 .
.
Рассмотрение вращательных степеней свободы проводится аналогично.
Таким образом, можно сделать общий вывод: в классической механике на каждую степень свободы молекулы приходится энергия, равная kT/2. Однако, такой вывод неверен в квантовой механике.
Поможем написать любую работу на аналогичную тему

