При статистическом методе для определения основной характеристики ![]() (X– совокупность координат и импульсов всех частиц системы) используются те или иные модели строения рассматриваемого тела
(X– совокупность координат и импульсов всех частиц системы) используются те или иные модели строения рассматриваемого тела ![]() .
.
Оказывается возможным нахождения общих свойств общих статистических закономерностей, которые не зависят от строения вещества и являются универсальными. Выявление таких закономерностей является основной задачей термодинамического метода описания тепловых процессов. Все основные понятия и законы термодинамики могут быть раскрыты на основе статистической теории.
Для изолированной (замкнутой) системы или системы в постоянном внешнем поле состояние называется статистически равновесным,если функция распределения ![]() не зависит от времени.
не зависит от времени.
Конкретный вид функции распределения![]() рассматриваемой системы зависит как от совокупности внешних параметров
рассматриваемой системы зависит как от совокупности внешних параметров ![]() , так и от характера взаимодействия с окружающими телами. Под внешними параметрами в данном случае будем понимать величины, определяемые положением не входящих в рассматриваемую систему тел. Это, например, объем системы V, напряженность силового поля и т.д. Рассмотрим два наиболее важных случая:
, так и от характера взаимодействия с окружающими телами. Под внешними параметрами в данном случае будем понимать величины, определяемые положением не входящих в рассматриваемую систему тел. Это, например, объем системы V, напряженность силового поля и т.д. Рассмотрим два наиболее важных случая:
1) Рассматриваемая система энергетически изолирована. Полная энергия частиц Е постоянна. При этом ![]() .Е можно включить в а, но выделение его подчеркивает особую роль Е. Условие изолированности системы при заданных внешних параметрах можно выразить равенством:
.Е можно включить в а, но выделение его подчеркивает особую роль Е. Условие изолированности системы при заданных внешних параметрах можно выразить равенством: ![]()
2) Система не замкнута – возможен обмен энергией. В этом случае нельзя найти ![]() , она будет зависеть от обобщенных координат и импульсов частиц окружающих тел. Это оказывается возможным, если энергия взаимодействия рассматриваемой системы с окружающими телами
, она будет зависеть от обобщенных координат и импульсов частиц окружающих тел. Это оказывается возможным, если энергия взаимодействия рассматриваемой системы с окружающими телами ![]() .
.
При этом условии функция распределения микросостояний ![]() зависит от средней интенсивности теплового движения окружающих тел, которую характеризуют температурой Т окружающих тел:
зависит от средней интенсивности теплового движения окружающих тел, которую характеризуют температурой Т окружающих тел: ![]() .
.
Температура также играет особую роль. Она не имеет (в отличие от а) аналога в механике: ![]() (не зависит от Т).
(не зависит от Т).
В состоянии статистического равновесия![]() не зависит от времени, неизменны и все внутренние параметры. В термодинамике такое состояние называют состоянием термодинамического равновесия.Понятия статистического и термодинамического равновесия эквивалентны.
не зависит от времени, неизменны и все внутренние параметры. В термодинамике такое состояние называют состоянием термодинамического равновесия.Понятия статистического и термодинамического равновесия эквивалентны.
Функция распределения микроскопической изолированной системы – микроканоническое распределение Гиббса
Случай энергетически изолированной системы. Найдем вид функции распределения ![]() для этого случая.
для этого случая.
Существенную роль при нахождении при функции распределения играют лишь интегралы движения ![]() – энергия,
– энергия, ![]() – импульс системы и
– импульс системы и ![]() – момент импульса. Лишь они являются контролируемыми.
– момент импульса. Лишь они являются контролируемыми.
Гамильтониану в механике отводится особая роль, т.к. именно функцией Гамильтона определяется вид уравнения движения частиц. Сохранение полного импульса и момента импульса системы при этом является следствием уравнений движения.
Поэтому выделяют именно такие решения уравнения Лиувилля, когда зависимость ![]() проявляется лишь через гамильтониан
проявляется лишь через гамильтониан![]() :
:
![]() .
.
Так как![]() ,
, ![]() .
.
Из всех возможных значений Х (совокупность координат и импульсов всех частиц системы) выделяются те, которые совместимы с условием ![]() . Константу Сможно найти из условия нормировки:
. Константу Сможно найти из условия нормировки:
![]() ,
,
где ![]() –площадь гиперповерхности в фазовом пространстве
–площадь гиперповерхности в фазовом пространстве ![]() , выделяемой условием постоянства энергии.
, выделяемой условием постоянства энергии.
Т.е. 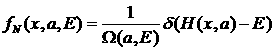 – микроканоническое распределение Гиббса.
– микроканоническое распределение Гиббса.
В квантовой теории равновесного состояния, так же существует микроканоническое распределение Гиббса. Введем обозначения: ![]() – полный набор квантовых чисел, характеризующих микросостояние системы частиц,
– полный набор квантовых чисел, характеризующих микросостояние системы частиц, ![]() – соответствующие допустимые значения энергии. Их можно найти, решая стационарное уравнение для волновой функции
– соответствующие допустимые значения энергии. Их можно найти, решая стационарное уравнение для волновой функции ![]() рассматриваемой системы.
рассматриваемой системы.
Функция распределения микросостояний в таком случае будет представлять собой вероятность для системы находиться в определенном состоянии: ![]() .
.
Квантовое микроканоническое распределение Гиббса может быть записанов виде:
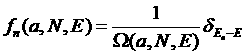 ,
,
где 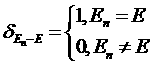 – символ Кронекера,
– символ Кронекера, ![]() – из нормировки:
– из нормировки: ![]() – число микросостояний с заданным значением энергии (а так же
– число микросостояний с заданным значением энергии (а так же ![]() ). Она называется статистическим весом.
). Она называется статистическим весом.
Из определения ![]() все состояния удовлетворяющие условию
все состояния удовлетворяющие условию ![]() имеют одинаковою вероятность, равную
имеют одинаковою вероятность, равную ![]() . Таким образом, в основе квантового микроканонического распределения Гиббса лежит принцип равных априорных вероятностей.
. Таким образом, в основе квантового микроканонического распределения Гиббса лежит принцип равных априорных вероятностей.
Функция распределения микросостояний системы в термостате – каноническое распределение Гиббса.
Рассмотрим теперь систему, обменивающуюся энергией с окружающими телами. Этому подходу с термодинамической точки зрения соответствует система, окруженная очень большим термостатом с температурой T. Для большой системы (наша система + термостат) можно использовать микроканоническое распределение, поскольку такая система может считаться изолированной. Будем полагать, что рассматриваемая система составляет малую, но макроскопическую ![]() часть большей системы с температурой Т и числом частицв ней
часть большей системы с температурой Т и числом частицв ней ![]() . То есть выполняется равенство (
. То есть выполняется равенство (![]() >>
>>![]() )
)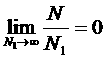 .
.
Будем обозначать переменные нашей системы через X, а переменные термостата через X1.
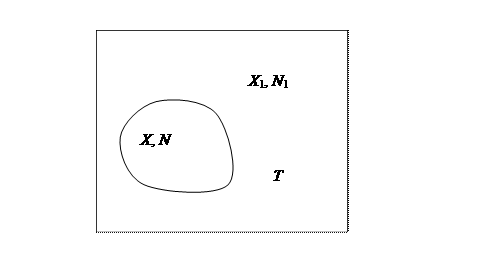
Тогда для всей системы запишем микроканоническое распределение:
![]() .
.
Нас будет интересовать вероятность состояния системы из Nчастиц при любых возможных состояниях термостата.Эту вероятность можно найти, проинтегрировав это уравнение по состояниям термостата
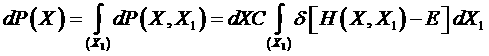 .
.
Функция Гамильтона системы и термостата может быть представлена в виде
![]() .
.
Будем пренебрегать энергией взаимодействия между системой и термостатом по сравнению, как с энергией системы, так и с энергией термостата. Это можно сделать, поскольку энергию взаимодействия для макросистемы пропорциональна площади ее поверхности, в то время как энергия системы пропорциональна ее объему. Однако пренебрежение энергией взаимодействия по сравнению с энергией системы не означает, что оно равно нулю, в противном случае постановка задачи теряет смысл.
Таким образом, распределение вероятностей для рассматриваемой системы можно представить в виде
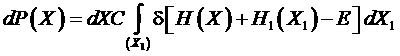 .
.
Перейдем к интегрированию по энергии термостата
![]() ,
,
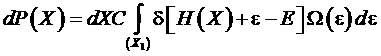 .
.
Отсюда, воспользовавшись свойством d-функции
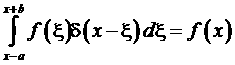 ,
,
получим
![]() .
.
Будем в дальнейшем переходить к предельному случаю, когда термостат очень велик. Рассмотрим частный случай, когда термостат представляет собой идеальный газ с N1 частицами с массой m каждая.
Найдем величину ![]() , которая представляет собой величину
, которая представляет собой величину
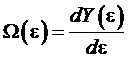 ,
,
где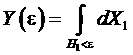 представляет собой объем фазового пространства, заключенного внутри гиперповерхности
представляет собой объем фазового пространства, заключенного внутри гиперповерхности ![]() . Тогда
. Тогда 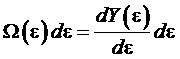 представляет собой объем гипершарового слоя (сравните с выражением для трехмерного пространства
представляет собой объем гипершарового слоя (сравните с выражением для трехмерного пространства 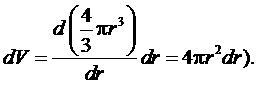
Для идеального газа область интегрирования дается условием
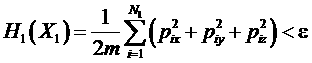 .
.
В результате интегрирования в указанных границах получаем объем 3N1-мерного шара с радиусом![]() , который будет равен
, который будет равен ![]() . Таким образом, имеем
. Таким образом, имеем
![]() .
.
Откуда имеем
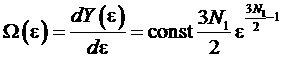 .
.
Таким образом, для распределения вероятностей имеем
![]() .
.
Перейдем теперь к пределу N1®¥ , однако, предполагая, что отношение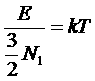 остается постоянным (так называемый термодинамический предел). Тогда получим
остается постоянным (так называемый термодинамический предел). Тогда получим
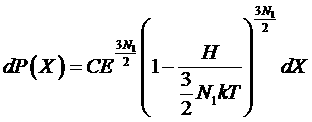 .
.
Принимая во внимание, что
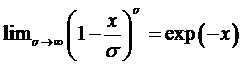 ,
,
получим
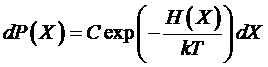 .
.
Тогда функция распределения системы в термостате может быть записана в виде
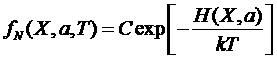 ,
,
где Снаходится из условия нормировки:
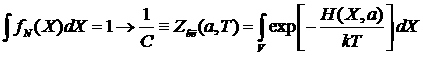 .
.
Функция ![]() называется классическим статистическим интегралом.Таким образом, функция распределения системы в термостате может быть представлена в виде:
называется классическим статистическим интегралом.Таким образом, функция распределения системы в термостате может быть представлена в виде:
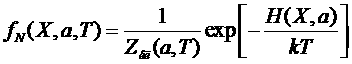
– это и есть каноническое распределение Гиббса(1901 г.).
В этом распределении Т характеризует среднюю интенсивность теплового движения – абсолютную температуру частиц окружающей среды.
Другая форма записи распределения Гиббса
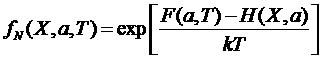 ,
,
![]() .
.
Далее мы увидим, что![]() совпадает со свободной энергией из термодинамики (энергия Гельмгольца).
совпадает со свободной энергией из термодинамики (энергия Гельмгольца).
При определении ![]() считались различными микроскопическими состояния, отличающиеся лишь перестановкой отдельных частиц.Это означает, что мы в состоянии следить за каждой частицей. Однако такое предположение приводит к парадоксу.
считались различными микроскопическими состояния, отличающиеся лишь перестановкой отдельных частиц.Это означает, что мы в состоянии следить за каждой частицей. Однако такое предположение приводит к парадоксу.
Выражение для квантового канонического распределения Гиббса, может быть записано по аналогии с классическим:
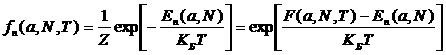 ,
,
![]() – статистическая сумма:
– статистическая сумма: 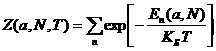 .
.
Она является безразмерным аналогом статистического интеграла. Тогда свободная энергия может быть представлена в виде:
![]() .
.
Рассмотрим теперь систему, находящуюся в термостате и способную обмениваться энергией и частицами с окружением. Вывод функции распределения Гиббса для этого случая во многом аналогичен выводу канонического распределения. Для квантового случая распределение имеет вид:
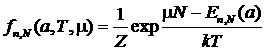
–это распределение называется Большое каноническое распределение Гиббса. Здесь μ – химический потенциал системы, который характеризует изменение термодинамических потенциалов при изменении числа частиц в системе на единицу.
Z – из условия нормировки:
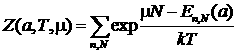 .
.
Здесь суммирование идет не только по квадратным числам, но и по всем возможным значениям числа частиц.
Другая форма записи: введем функцию ![]() , но так как ранее получено
, но так как ранее получено 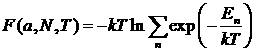 из термодинамики
из термодинамики ![]() , где
, где ![]() – большой термодинамический потенциал.В результате получим
– большой термодинамический потенциал.В результате получим
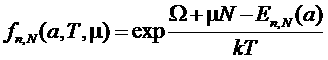 .
.
Здесь ![]() –среднее значение числа частиц.
–среднее значение числа частиц.
Классическое распределение аналогично.
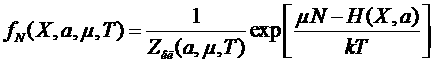 .
.
Распределения Максвелла и Больцмана
Каноническое распределение Гиббса устанавливает (при заданной ![]() ) явный вид функции распределения значений всех координат и импульсов частиц (6N-переменных). Но такая функция
) явный вид функции распределения значений всех координат и импульсов частиц (6N-переменных). Но такая функция ![]() очень сложна. Часто достаточно более простых функций.
очень сложна. Часто достаточно более простых функций.
Распределение Максвелла для идеального одноатомного газа. Каждую молекулу газа мы можем считать «рассматриваемой системой», принадлежащими к термостату. Поэтому вероятность какой-либо молекуле иметь импульсы в заданных промежутках ![]() дается каноническим распределением Гиббса:
дается каноническим распределением Гиббса: 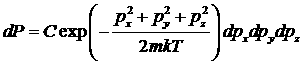 .
.
Заменяя импульсы скоростями, и используя условия нормировки, получим
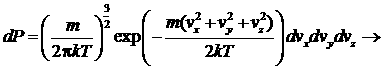
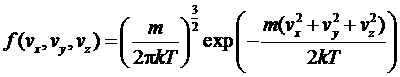 – функция распределения Максвелла по компонентам скорости. Легко получить распределение и по модулю.
– функция распределения Максвелла по компонентам скорости. Легко получить распределение и по модулю.
В любой системе, энергия которой равна сумме энергий отдельных частиц имеет место выражение, аналогичное максвелловскому. Это распределение Максвелла-Больцмана. Опять будем считать, что «системой» является одна какая-либо частица, остальные же играют роль термостата. Тогда вероятность состояния этой избранной частицы при любом состоянии остальных дается каноническим распределением: 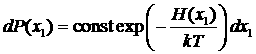 ,
, ![]() .По остальным величинам
.По остальным величинам![]() …
…![]() проинтегрировали
проинтегрировали
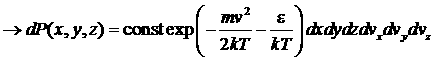 .
.
Поможем написать любую работу на аналогичную тему

