Однако в реальных условиях все переменные, как правило, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при условии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества переменных, влияние которых исключается, частные коэффициенты корреляции могут быть различного порядка: при исключении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влияния двух переменных – второго порядка и т.д. Парный коэффициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.
Частный коэффициент корреляции первого порядка между признаками х1 и у при исключении влияния признака х2 вычисляют по формуле:
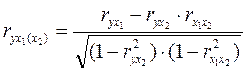 (7)
(7)
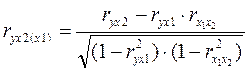 (8)
(8)
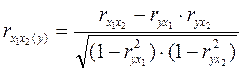 (9)
(9)
где r – соответствующие парные коэффициенты корреляции.
Поможем написать любую работу на аналогичную тему

