Множественная регрессия - Ответы по эконометрике

Уравнение множественной регрессии имеет вид:

Линейная множ регр

Метод наименьших квадратов для оценки параметров множественной линейной регрессии

Суть метода состоит в минимизации суммы квадратов отклонений фактических значений результатного признака от его расчетных значений, т.е.:

.

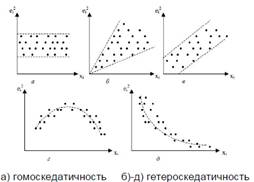
Для применения метода наименьших квадратов требуется, чтобы дисперсия остатков модели являлась гомоскедатичной, т.е. для срезов значений фактора xj и xi дисперсия остатков должна быть постоянной. При нарушении данных условий процесс является гетероскедатичным.

Наиболее популярные методы и критерии выявления скедатичности:

1) визуальный анализ отклонений;

2) тест ранговой корреляции Спирмена;

3) тест Пака;

4) тест Глейзера;

5) тест Гольдфельда-Квандта.

Тест Гольдфельда-Квандта

Предположения:

- дисперсия остатков <j(Sj) пропорциональна х];

- Sj имеет нормальное распределение;

- автокорреляция остатков отсутствует.

Этапы применения теста:

1. все T наблюдений упорядочиваются по величине х];

2. вся упорядоченная выборка разбивается на три группы размерности к , (T - 2k) и к причем (T -2к)> m (число параметров в модели);

3. получаем: первая группа размерности к - имеет большее значение фактора х];

вторая группа размерности (T - 2к) - средние значения х] и третья группа размерности к наибольшие значения х];

4. среднюю группу исключают из рассмотрения. По двум другим строят уравнение регрессии (по каждой группе отдельно), рассчитывают значения остаточной суммы квадратов

5. Если предположение о пропорциональности дисперсии остатков и фактора выполнено, то S1 < S3.

6. Для сравнения дисперсии используется F-статистика:

F13 = S3/S1

При сделанных предположениях полученная с.в. F13 имеет распределение Фишера с k-m-1 степенями свободы.

Правило А! Если F13 > Ftabl, то гипотеза об гомоскедатичности отклоняется, т.е. дисперсия гетероскедатична. Чем больше величина F13 превышает табличное значение критерия, тем больше нарушена предпосылка о равенстве остаточных дисперсий.

Под  мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных, которая приводит к линейной зависимости нормальных уравнений.

Существует несколько способов для определения наличия или отсутствия мультиколлинеарности.

Один из подходов заключается в  анализе матрицы коэффициентов парной корреляции. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8.

Другой подход состоит в исследовании матрицы  Х'Х.  Если определитель матрицы Х'Х  близок к нулю, то это   свидетельствует о наличии мультиколлинеарности.

Оценка значимости коэффициентов регрессии с помощью критерия Стюдента (t-критерия) осуществляется путем сравнения

где mbj - стандартные ошибки коэффициентов bj модели множественной регрессии.

Правило! Если bj > ttabl  - то коэффициент регрессии является значимым, иначе влияние фактора xj в следствие малой значимости коэффициента bj и низкой степени статистической значимости может не учитываться в модели.