Методы отбора факторов

“Оптимальный” состав факторов, включаемых в эконометрическую модель, является одним из основных условий ее “хорошего” качества, понимаемого и как соответствие формы модели теоретической концепции, выражающей содержание взаимосвязей между рассматриваемыми переменными, и как точность предсказания на рассматриваемом интервале времени t=1, 2,..., Т наблюдаемых значений переменной уt уравнением f(a, xt).

Проблема выбора “оптимальных” факторов обычно решается на основе содержательного и количественного (статистического) анализа тенденций рассматриваемых процессов.

На этапе содержательного анализа решается вопрос о целесообразности включения в модель тех или иных факторов, исходя из “здравого” смысла. В макроэкономических исследованиях состав факторов, как правило, определяется на основании допущений экономической теории. Пример – двухфакторные производственные функции типа Кобба-Дугласа, постоянной эластичности замены, которые строятся в предположении, что объем выпуска (производства) экономической системы в основном зависит от размеров используемых основных фондов и количества затраченного труда. Далее, как это было отмечено в разделе 1.2, производственная  функция типа Кобба-Дугласа учитывает предположение о  постоянной эластичности выпуска по каждому из факторов, а функция постоянной эластичности замены – свойство постоянства замещения изменения одного из этих факторов изменением другого.

Здесь следует иметь в виду, что на этапе содержательного анализа обычно решается проблема установления самого факта наличия взаимосвязей между явлениями. Однако, как было отмечено в разделе 1.2,  каждое из явлений может быть выражено разными факторами и даже их комбинациями. Поэтому в ряде исследований на основании содержательного анализа однозначно состав независимых переменных  модели определить практически невозможно. Могут существовать их альтернативные наборы. Например, для исследования закономерностей динамики производительности труда на заводе могут быть отобраны, исходя из содержательной целесообразности, следующие факторы: объем основных фондов, электровооруженность труда, фондовооруженность труда, численность рабочей силы, ее квалификация. При этом квалификация как явление может выражаться разными показателями, например, средним  уровнем образования работников,  их усредненным квалификационным разрядом и т. п. Кроме того, можно ожидать, что показатели электровооруженности, фондовооруженности труда, объема основных фондов характеризуют одно и то же явление – изменение материально-технической оснащенности производственного процесса. Таким образом, некоторые из рассматриваемых в таком исследовании показателей, выражающих количественные характеристики независимых переменных, относятся к  сходным явлениям.

Аналогично, в исследованиях заболеваемости населения каждая из определяющих это явление причин может быть количественно отображена разными факторами. Например, уровень жизни – среднедушевым доходом, обеспеченностью жильем, розничным товарооборотом в расчете на одного жителя и т. п.; климатические условия – среднегодовой температурой, числом солнечных дней в году, влажностью и рядом других показателей; качество окружающей среды – среднегодовыми объемами выбросов и сбросов загрязняющих веществ, среднегодовыми уровнями их концентрации в воздухе, воде и почве и т. д., уровень медицинского обслуживания – количеством медицинских работников в расчете на одного жителя; числом койко-мест в лечебных заведениях на одного жителя и другими показателями.

Несложно заметить, что  факторы, выражающие одну и ту же причину, могут быть тесно взаимосвязаны между собой. Так, например, уровень розничного товарооборота в основном зависит от среднедушевого дохода; концентрация загрязняющих веществ –  от объемов их выбросов; наблюдается взаимосвязь между обеспеченностью населения медицинским персоналом и койко-местами в лечебных учреждениях и т. д. Вследствие этого, одновременное включение таких факторов в модель вряд ли целесообразно, поскольку таким образом одна и та же причина будет учтена дважды.

 В результате в общем случае на этапе обоснования эконометрической модели исследователи могут столкнуться с проблемой выбора наиболее предпочтительного состава независимых факторов среди ряда альтернативных вариантов.  Можно выделить два основных подхода к решению этой проблемы. Первый из них предполагает априорное (до построения модели) исследование характера и силы взаимосвязей между рассматриваемыми переменными, по результатам которого в модель включаются факторы, наиболее значимые по своему “непосредственному” влиянию на зависимую переменную уt. И, наоборот, из модели исключаются факторы, которые, либо малозначимы с точки зрения силы своего влияния на переменную уt, либо их сильное влияние на нее можно трактовать как индуцированное  взаимосвязями с другими экзогенными переменными.

Второй подход к отбору независимых факторов можно назвать апостериорным. Он предполагает первоначально включить в модель все отобранные на этапе содержательного анализа факторы. Уточнение их состава в этом случае производится на основе анализа характеристик качества построенной модели, одной из групп которых являются и показатели, выражающие силу влияния каждого из факторов на зависимую переменную уt.

Рассмотрим особенности процедуры отбора факторов на основе использования каждого из этих подходов более подробно.

В  основе “априорного” подхода лежат следующие предположения. 

1. Сильное влияние фактора на зависимую переменную должно подтверждаться и определенными количественными характеристиками, важнейшей из которых является их парный линейный коэффициент корреляции, выборочное значение которого рассчитывается на основании имеющейся информации  по формуле:

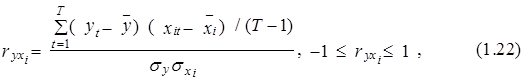
где   – средние значения соответствующих переменных, а  – их среднеквадратические отклонения.

Логика использования коэффициента парной корреляции при отборе значимых факторов на практике состоит в следующем. Если значение достаточно велико, т. е. >r1,  где    r1 – некоторый эмпирический рубеж (на практике r1»0,5-0,6), то можно говорить о наличии существенной линейной связи между переменными у и хi  или о достаточно сильном влиянии  хi  на у. Чем больше абсолютное значение  ,  тем сильнее это влияние (положительное или отрицательное, в зависимости от знака r).

Здесь следует иметь в виду, что значение    должно рассчитываться с учетом формы преобразования у и хi  в модели. Например, если у~1/хi, то и коэффициент корреляции определяется между у и ui =1/хi   и т.п.

2. Если два и более факторов выражают одно и то же явление (см. рассмотренные выше примеры), то, как правило, между ними также должна существовать достаточно сильная взаимосвязь. На это может указать выборочное значение их парного коэффициента корреляции

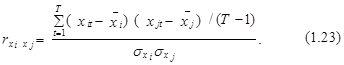
На практике взаимосвязь между факторами признается существенной, если  >r2,  где r 2  »0,8–0,9. В таких ситуациях один из этих факторов целесообразно исключить из модели, с тем, чтобы одна и та же причина не учитывалась дважды. Однако повторим, что такое исключение следует проводить только в тех случаях, когда факторы выражают одно и то же явление.

Отметим, что приведенные рубежные значения (в первом случае – 0,5–0,6; во втором – 0,8–0,9) достаточно условны. В каждом конкретном случае они устанавливаются индивидуально. При их выборе существенную роль играет интуиция исследователя. Обычно считается, что, если для фактора хi  <0,5, то при большом числе других достаточно значимых факторов, информацией, которую содержит в себе фактор хi  относительно изменчивости переменной у, можно пренебречь. Иногда же, наоборот, если состав факторов не слишком широк, и фактор хi     выражает существенное с точки зрения теории явление, то исследователь, стремясь не потерять информацию о закономерностях изменчивости переменной у, может оставить его в модели и при меньшем значении выборочного коэффициента корреляции (=0,3–0,4).

Здесь следует еще раз подчеркнуть, что при таком отборе, основанном на эмпирике и интуиции, обычно не принимается во внимание точность оценки выборочных коэффициентов корреляции, которая растет с увеличением выборки, т. е. значения Т. При фиксированном значении Т точность оценок всех коэффициентов примерно одинакова. Логика такого отбора в большей степени ориентирована на содержательную сторону проблемы учета взаимосвязей между переменными модели.

Значительно усложняет проблему отбора факторов явление ложной корреляции, которое характеризуется достаточно высокими по абсолютной величине значениями коэффициентов парной корреляции у процессов, с содержательной точки зрения между собой никак не связанных. Иными словами, большие значения парных коэффициентов корреляции могут иметь место и в тех случаях, когда тенденции рассматриваемых процессов совпали случайно, при отсутствии между ними логически обоснованной взаимосвязи.

Примерами ложных корреляций являются совпадающие тенденции роста потребительских расходов в постоянных ценах и роста потребительских цен, роста выпуска продукции и потребления алкоголя и т. п.

Ложная корреляция может помешать при построении “правильной” модели по двум причинам. Во-первых, в модель случайно могут быть введены незначимые с содержательной точки зрения факторы, характеризующиеся значимыми величинами . Во-вторых, из модели могут быть исключены значимые с точки зрения влияния на у факторы, в отношении которых ошибочно признана гипотеза о том, что они выражают то же явление, что и другой фактор (факторы), уже включенный в эту модель.

Среди основных причин включения в модель переменных с ложной корреляцией часто называют ненадежность информации, используемой при определении значений факторов в различные моменты времени, трудности формализации факторов, имеющих качественный характер, неустойчивость тенденций изменения рассматриваемых переменных, неправильную форму взаимосвязи между ними и т. п.

Еще раз отметим, что основной путь, придерживаясь которого можно избежать ошибок, связанных с понятием “ложной корреляции”, связан с проведением качественного анализа проблемы, направленного на обоснование адекватного ей содержания и формы модели. При этом можно предложить и некоторые общие рекомендации, которых целесообразно придерживаться, следуя этим путем:

1.   Число факторов, включаемых в модель, не должно быть слишком велико. Их увеличение может свести к минимуму ее практическую ценность, так как в этом случае модель начинает отражать не закономерность развития на фоне случайности, а саму случайность.

2.   Простота модели в значительной степени является гарантией ее адекватности, поскольку более сложные зависимости часто априорно трудно уловимы на ограниченном временном интервале, но в то же время они допускают аппроксимацию достаточно простыми функциями. Иными словами, сложная модель может в большей степени выражать второстепенные взаимосвязи между переменными в ущерб основным.

При апостериорном подходе уточнение состава факторов эконометрической модели осуществляется на основе анализа значений ряда качественных характеристик уже построенного ее варианта. Одну из групп таких характеристик, являющихся наиболее важными при отборе факторов, образуют значения критерия Стьюдента, рассчитываемые для коэффициентов при каждом из факторов модели. С помощью этого критерия проверяется гипотеза о значимости влияния фактора на зависимую переменную у.

Здесь следует отметить, что окончательное решение о целесообразности оставления фактора или его удаления из модели принимается на основе анализа всего комплекса ее характеристик качества с учетом содержательной стороны проблемы взаимосвязей между зависимой и независимыми переменными. Вопросы их расчета и логика принятия такого решения будут изложены в разделе 1.4. Критерий Стьюдента лишь указывает на те факторы, которые с точки зрения статистики являются возможными (целесообразными) кандидатами на удаление.

Заметим, что ответ на вопрос о целесообразности включения в число факторов-кандидатов на удаление каждой из независимых переменных хi, i=1, 2,..., n, при апостериорном подходе решается уже после того, как оценены значения коэффициентов модели и определены некоторые дополнительные характеристики точности полученных оценок. Вопросы определения этих характеристик рассмотрены в главе II.

Будем считать, что с помощью какого-либо из методов, рассмотренных в главе II, например, метода наименьших квадратов, найдены численные значения оценок параметров a0, a1,..., an  линейной эконометрической модели (1.2)*. Как будет показано в главе II, эти оценки являются выборочными (определенными по наблюдаемой выборке исходных данных). Согласно этому они рассматриваются как случайные величины, распределенные «приблизительно» по нормальному закону с соответствующими математическими ожиданиями и дисперсиями (среднеквадратическими отклонениями). Методы оценивания параметров позволяют определить и значения дисперсий полученных оценок s(ai ).

Логика использования критерия Стьюдента при выявлении факторов-кандидатов на удаление из уже построенного варианта модели основывается на следующих его свойствах. Напомним, что случайная величина t, определенная согласно выражению

распределена по закону Стьюдента с k степенями свободы, k  – объем выборки;  – выборочное среднее некоторой случайной величины z; – ее математическое ожидание (среднее по генеральной совокупности);  – среднеквадратическое отклонение выборочного среднего.

Таким образом, с помощью критерия Стьюдента может быть проверена гипотеза о равенстве найденного выборочного среднего предполагаемому значению математического ожидания. На практике обычно эта гипотеза принимается, если оказывается, что для расчетного значения критерия Стьюдента выполняется следующее соотношение t<t*( k), где t*( k) – табличное значение критерия Стьюдента, соответствующее доверительной вероятности  р*  и числу степеней свободы k*.

При определении значимости (незначимости) i-го фактора принимаются во внимание следующие обстоятельства. Оценка соответствующего ему коэффициента ai, полученная с использованием выбранного метода оценивания параметров, приравнивается к выборочному среднему . Для незначимого фактора логично предположить, что истинное значение ai  равно нулю, т. е. математическое ожидание оценки равно нулю М=0.

С учетом этого расчетное значение критерия Стьюдента при проверке гипотезы о значимости i-го фактора определяется по следующей формуле:

где ½ai½– абсолютное значение оценки коэффициента ai  в модели, характеризующее степень влияния i-го фактора на результирующий показатель; s(ai) – среднеквадратическая ошибка оценки этого коэффициента, определяемая на этапе его расчета (см. главу II).

Если имеет место соотношение

                                      ti £t*,                                                              (1.26)

то влияние фактора хi  на переменную у можно признать незначимым (недостаточно значимым), где t* – табличное значение критерия Стьюдента.

Если же  ti >t*, то логичен вывод, что значение ai может рассматриваться как отличная от нуля оценка i-го коэффициента модели, и, таким образом, влияние фактора хi  на переменную у целесообразно признать значимым.

Если фактор хi признается незначимым, то его “целесообразно”* удалить из модели. Эта операция приводит к уменьшению общего количества независимых переменных в модели.

Таким образом, можно предложить следующую поэтапную процедуру построения окончательно варианта модели на основе апостериорного подхода:

 1.  В исходный вариант модели включаются все факторы, отобранные в ходе содержательного анализа проблемы. Для этого варианта рассчитываются значения оценок коэффициентов модели, их среднеквадратические ошибки и значения критериев Стьюдента (выражение (1.25)).

2.   Из модели удаляют незначимый фактор, характеризующийся наименьшим значением ti (при условии, что ti £t*), и таким образом формируют новый вариант модели с уменьшенным на один числом факторов. Заметим, что в модели может быть несколько незначимых факторов. Однако все их одновременно удалять не следует. Возможно, что незначимость большинства из них обусловлена влиянием “наихудшего” из незначимых факторов и на следующем шаге расчетов эти факторы окажутся значимыми.

3.   Процесс отбора факторов можно считать законченным, когда остающиеся в модели факторы являются значимыми, Если полученный вариант модели удовлетворяет и другим критериям ее качества, то процесс построения модели можно считать завершенным в целом.

В противном случае целесообразно попытаться сформировать другой альтернативный вариант модели, отличающийся от предыдущего либо составом факторов, либо формой их взаимосвязи с зависимой переменной у.

Здесь сразу следует отметить, что каждый из этих подходов имеет свои преимущества и недостатки.

“Априорный” путь отбора факторов не обладает достаточной обоснованностью. Он в большей степени использует “прямые” количественные индикаторы “силы” взаимосвязей между рассматриваемыми величинами и не принимает во внимание в полной мере особенности комплексного влияния независимых факторов на переменную уt, т. е. своеобразные эффекты “эмерджентности” такого влияния. Этот эффект выражается в том, что совокупное воздействие нескольких факторов на переменную уt может значительно отличаться от суммы воздействий каждого из них именно в силу наличия внутренних взаимосвязей между независимыми переменными.

Вместе с тем использование априорного подхода часто позволяет уточнить некоторые предварительные альтернативные варианты наборов независимых факторов, проверить исходные предпосылки модели относительно правильности выбора формы взаимосвязей между ними.

“Апостериорный” подход к отбору факторов на первый взгляд является более предпочтительным как раз из-за того, что целесообразность включения каждого из факторов в эконометрическую модель определяется на основании всего комплекса взаимосвязей между вошедшими в модель переменными. Однако, когда общее количество факторов достаточно велико, то нет никаких гарантий, что множество несущественных, а то и ложных взаимосвязей между ними не будет превалировать над основными. В результате может оказаться, что в числе первых кандидатов на исключение будут “названы” наиболее важные, значимые с точки зрения влияния на переменную уt  факторы.  Поэтому в сложных случаях, т. е. при наличии большого числа отобранных для включения в модель  на этапе содержательного анализа факторов, специалисты рекомендуют сочетать при формировании их “оптимального” состава оба подхода – априорный и апостериорный.

Согласно этим рекомендациям с помощью методов “априорного” отбора, используя при этом и содержательный анализ, формируются альтернативные варианты включаемых в модель наборов факторов. Далее с помощью методов “апостериорного” отбора эти наборы уточняются и соответствующие им варианты моделей сопоставляются по ряду характеристик их качества. Предполагается, что лучший из вариантов модели содержит и “оптимальный” набор факторов.

В результате процедура отбора факторов в эконометрическую модель превращается в перебор некоторого множества их приемлемых сочетаний, сформированных на базе “априорного” подхода.

Перебирая различные варианты составов независимых факторов, рассматривая возможные виды их взаимосвязей с зависимой переменной, исследователь формирует и разные варианты (модификации) эконометрической модели для описания рассматриваемых процессов. В этом случае возникает проблема выбора “оптимального” или наиболее “рационального” среди них. Обычно эта проблема решается на основе аналитического сопоставления статистических характеристик качества построенных вариантов, рассчитываемых уже при известных значениях оценок их параметров.