Процедура оценки параметров по методу наименьших квадратов

Метод наименьших квадратов (МНК) является одним из наиболее разработанных и распространенных вследствие своей относительной простоты и эффективности методов оценки параметров линейных эконометрических моделей. Он не предъявляет жестких требований к закону распределения ошибок моделей. Вследствие этого оценки коэффициентов моделей, полученные на основе МНК, не зависят от фактического (или предполагаемого) закона распределения. Хотя обычно закон распределения ошибки, если его знание необходимо для проверки качества модели, свойств ее параметров и т. п., предполагается нормальным. При этом в “классическом” варианте МНК, как это будет показано далее, в отношении свойств ошибки модели et  выдвигаются следующие предположения:

– ошибка имеет нулевое математическое ожидание, M=0;

– ее дисперсия конечна и постоянна, se2=const;

– автокорреляционные связи в ряду ошибки отсутствуют,    т. е. r1=r2=...=0, где ri  – коэффициент автокорреляции рядов et и et–i, i=1,2,... ;

– ряд значений ошибки статистически  не связан с рядами значений независимых переменных модели.

Рассмотренные предположения определяют ошибку модели как процесс белого шума с ковариационной матрицей ее вектора ошибки, имеющей следующий вид: Cov(e)=se2×Е.

Рассмотрим общую схему процедуру оценки параметров линейной эконометрической модели на основе МНК более подробно. Такая модель в общем виде была представлена уравнением (1.2):

yt=a0+a1 х1t +...+anхnt +et.

Исходными данными при оценке параметров  a0, a1,..., an являются измеренные (наблюдаемые) значения зависимой переменной, которые можно представить в виде вектора-столбца,  

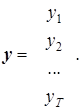
Наблюдаемые значения независимых переменных объединим в матрицу следующего вида:

                                    Х =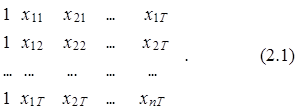          

Cвое название МНК получил, исходя из смыслового содержания критерия, которому должны удовлетворять полученные на его основе оценки параметров эконометрической модели:

сумма квадратов значений фактической ошибки модели должна быть минимальной.

Иными словами, найденные с помощью МНК оценки a0, a1,..., an,  обеспечивают минимум следующей квадратичной формы на множестве всех других комбинаций значений таких оценок:

где et  – значение фактической ошибки модели в момент t=1,2,..., Т,  полученное после подстановки в выражение (1.2) вместо неизвестных истинных значений параметров a0, a1,..., an  их оценок a0, a1,..., an.

Оптимальные по данному критерию значения оценок в этом случае могут быть найдены путем решения следующей системы так называемых “нормальных” уравнений, вытекающей из условия равенства нулю частных производных функции s2 (a0, a1,..., an) по своим параметрам в точке минимума:

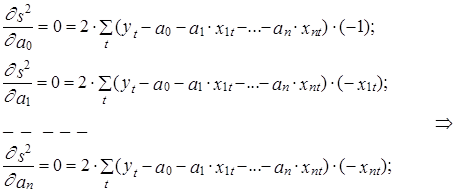
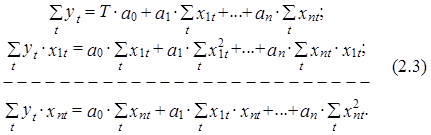
В системе (2.3) неизвестными являются оценки параметров a0, a1,..., an, а ее известные коэффициенты сформированы на основе исходных данных и представлены в виде следующих сумм:  i,j=1,2,..., п. Решения, получаемые на основе развернутой формы системы (2.3), достаточно громоздки, и поэтому в дальнейшем в математических выкладках общего характера будем использовать векторно-матричную форму представления ее составляющих.

Векторно-матричная форма записи линейной эконометрической модели (1.2) имеет следующий вид:

                                     у=Х×a+e,                                     (2.4)

где у – вектор-столбец, состоящий из Т компонент; Х – матрица размера Т´(п+1) (если в модели присутствует “свободный” коэффициент a0); a=(a0, a1,..., an)¢– вектор-столбец параметров, состоящий из п+1-й компоненты; e – вектор-стобец ошибки модели, состоящий, как и вектор у, из Т компонент.

Соответственно векторно-матричный вариант модели, в котором вместо неизвестных истинных коэффициентов a  и ошибок e  используются их оценки, т. е. вектора а и е, запишем в следующем виде:

                                     у=Х×а+е,                                     (2.5)

где а=(а0, а1,..., аn)¢, е=(е1, е2,..., еТ)¢– вектора значений оценок коэффициентов линейной эконометрической модели и значений ее фактической ошибки соответственно.

Сумму квадратов значений ошибки s2 можем представить в виде скалярного произведения вектора-строки е¢  на вектор-столбец е. Проводя несложные преобразования с учетом правил произведения векторов и матриц, получим следующий результат:

s2 =(е¢, е)=(у–Х×a)¢(у–Х×a)= у¢у–a¢Х¢у–у¢Хa+a¢Х¢Хa=

=у¢у–2a¢Х¢у+a¢Х¢Хa.                           (2.6)

При проведении преобразований учитывалось правило транспонирования векторно-матричного произведения (z×W)¢=(W¢×z¢).

Условие (2.3) в векторной форме записи приобретает следующий вид:

                                 ¶s2/¶a=0.                                     (2.7)

Заметим, что в выражении (2.7) операция дифференцирования осуществляется по вектору.

С учетом выражения (2.6) уравнение (2.7) приводится к следующему виду:

         ¶s2/¶a=¶(у¢у–2a¢Х¢у+a¢Х¢Хa)/¶a=–2Х¢у+2Х¢Хa=0

или

Х¢Хa=Х¢у.

Откуда следует, что “оптимальный” вектор оценок параметров a определяется на основе следующего векторно-матричного выражения:

                                      a=(Х¢Х)–1×Х¢у.                                             (2.8)

Все переменные в правой части выражения (2.8) являются известными – это исходные данные, сведенные в матрицу Х  и вектор у.