Особенности обоснования формы эконометрической модели

Основные подходы к решению проблем первого этапа исследования в значительной степени базируются на методах содержательного анализа закономерностей рассматриваемых процессов, подкрепляемых по мере необходимости методами общей и математической статистики.

Дело в том, что в практических исследованиях на предварительном этапе вид функционала эконометрической модели (1.1) и точный состав включенных в нее факторов могут быть априорно не известны. Часто имеются несколько альтернативных их вариантов, среди которых необходимо выбрать наиболее “приемлемый”. При этом “приемлемость” может отражать как требования экономической теории, так и необходимые ограничения по точности аппроксимации функционалом f(a, xt) исходного ряда зависимой переменной yt, t =1, 2,..., Т.

В этой связи прежде чем подойти к решению задач первого этапа, необходимо сформировать хотя бы предварительные исходные предпосылки относительно конкретного состава независимых переменных хi, вида функционала, связывающего их с зависимой переменной у. При этом исследователь может использовать различного рода “теоретические гипотезы”, как экономического, так и математического содержания в отношении вида функционала, свойств процессов yt , хit и e t.

Состав переменных хi и форма функционала f могут отражать либо экономическую концепцию, лежащую в основе взаимосвязи между зависимой и независимыми переменными, либо эмпирические (т. е. выявленные в ходе конкретных исследований) взаимосвязи между ними.

Исходными данными, необходимыми для построения эконометрической модели, являются известные наборы (массивы) значений зависимой переменной у и независимых факторов хi. При этом могут использоваться два принципиально различных типа исходных информационных массивов – статический и динамический. Статический массив представляет собой значения результирующей (зависимой, объясняемой и т.п.) переменной у и влияющих на нее факторов (независимых, объясняющих переменных) хi, имевших место у объектов однородной совокупности в определенный период времени. Примером таких объектов являются однотипные промышленные предприятия (заводы одной отраслевой направленности). В качестве у в практических исследованиях часто рассматриваются показатели производительности труда, объемов выпускаемой продукции и некоторые другие. В качестве хi – влияющие на уровень этих показателей факторы – объемы используемых фондов, численность и квалификация рабочей силы и т.п.

Приведем другой пример статической информации, характерной для социальных исследований. В качестве у рассматриваются показатели заболеваемости (смертности) населения в регионах страны. Их уровень в каждом из регионов определяют значения независимых факторов, отражающих достигнутый материальный уровень жизни, климатические условия, состояние окружающей среды и т. п. В этом случае необходимая для построения эконометрической модели информация собирается по совокупности регионов страны за фиксированный промежуток времени (год).

В общем случае будем считать, что необходимая для построения эконометрической модели базового типа (1.1) статическая информация выражается следующими массивами взаимосоответствующих наборов данных:

y1 « х11 х21 ... хi1 ... хn1 ;

y2 « х12 х22 ... хi2 ... хn2;

— — — — — — — — —

yj « х1j х2j ... хij ... хnj;

— — — — — — — — —

yN « х1N х2N ... хiN ... хnN,

где yj – уровень зависимой переменной на j-м объекте совокупности; хij – уровень фактора i-го фактора на j-м объекте совокупности; i=1, 2,..., n; j=1, 2,..., N.

В общем случае эконометрическая модель, использующая динамическую информацию, связывает значения некоторой зависимой переменной yt в моменты времени t cо значениями независимых переменных (факторов) хit, рассматриваемых в те же моменты времени (или в предшествующие)*, t=1,2,..., Т. Такая информация может отражать, например, уровни производительности труда на одном из заводов и определяющих их значения факторов в последовательные периоды времени.

Внимание!

Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.

Расчет стоимости Гарантии Отзывы

Исходная информация для построения эконометрических моделей может быть и смешанного типа. Например, она выражает уровни интересующих переменных по группе заводов за ряд лет.

Несложно заметить, что принципиального различия между статическим, динамическим и смешанным массивами не существует. Индекс t, в частности, может обозначать единицу совокупности (объект), так что набор y1, y2,..., yT может рассматриваться как выборка из Т заводов (регионов) и наоборот, индекс j=1, 2,..., N может обозначать время. Это же относится и к независимым переменным хij и хit. Вследствие этого в дальнейшем при изложении материала (если это не оговорено специально) для определенности будем использовать динамические индексы.

При формировании исходной информации для эконометрической модели чрезвычайно важной проблемой является выбор показателей, адекватных сущности исследуемых явлений. И здесь следует обратить внимание на определенную подмену понятий, которая обычно происходит на первом этапе построения модели при переходе от содержательного анализа явлений к формированию отражающих их уровни количественных характеристик (показателей).

В ходе содержательного анализа явление часто рассматривается на качественном уровне. При этом специалисты оперируют достаточно обобщенными понятиями, например, заболеваемость, уровень медицинского обслуживания, качество и уровень жизни, климат, качество рабочей силы и т. п. В этой связи, заметим, что часто эконометрическая модель строится именно для выражения закономерности, существующей между явлениями. Однако при построении модели используется исходная информация, наборы показателей, которые выражают эти явления, их свойства, тенденции в виде количественных характеристик. Вследствие этого желательно, чтобы такое «выражение» было в некотором смысле как можно более “точным”.

Для традиционных направлений исследований проблема обоснования состава показателей обычно считается решенной. Например, в исследованиях производительности труда, макроэкономическом анализе обычно рассматриваются уже устоявшиеся наборы показателей, значения которых публикуются в статистических сборниках, научных отчетах и т. п. Их примером являются выработка на одного работающего как показатель, выражающий явление “производительность труда”, объемы ВВП (показатель результативности экономики), объем основных фондов (показатель уровня материальной обеспеченности производственного процесса, экономики) и т.д.

Вместе с тем, в ряде областей эконометрических исследований такие системы показателей не могут быть сформированы столь однозначно. Часто одно и то же явление может быть выражено альтернативными вариантами показателей. Например, общий показатель заболеваемости в регионе за год может быть выражен суммарным числом заболеваний населения в течение этого периода времени. С другой стороны, в качестве меры заболеваемости может выступать и показатель, выраженный в виде суммарного количества дней продолжительности болезней.

Однако в обоих этих случаях не учитывается степень тяжести болезни. Попытка такого учета приводит к необходимости расчета средневзвешенного показателя заболеваемости, но здесь сразу возникает проблема обоснования адекватных “весов”. Тяжесть болезни может определяться, например, по степени ее опасности, рассчитываемой как доля обусловленных ею смертных случаев в общем их количестве; на основании субъективного показателя “дискомфортности” состояния больного и т. п.

Аналогичные проблемы должны быть решены при обосновании показателей климата. Для этих целей обычно используются средняя температура воздуха, влажность, число солнечных дней в году и т. п., а также построенные на их основе некоторые комплексные характеристики.

Заметим, что в отсутствие объективных данных в эконометрических исследованиях допускается замена одного показателя другим, косвенно отражающим то же явление. Например, среднедушевой доход как показатель материального уровня жизни может быть заменен на среднегодовой товарооборот на одного жителя региона и т. п.

Неправильный выбор показателя, представляющего рассматриваемое явление в модели, может существенно повлиять на ее качество. В этой связи к проблеме обоснования состава показателей (переменных) эконометрической модели на практике следует относиться с предельным вниманием.

Предположим, что общее число независимых факторов, которые целесообразно включить в модель, равно n, i=1, 2,..., n, и на основе измеренных значений всех переменных в моменты времени t=1, 2,..., T был сформирован массив исходных данных, который будет рассматриваться в качестве информационной основы для построения эконометрической модели.

Данный массив образован вектором-столбцом значений зависимой переменной y=(y1, y2, ... , yT)¢** и матрицей значений независимых переменных

Х =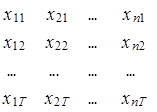

размерностью T´n, таким образом, что каждому элементу yt вектора y соответствует строка матрицы Х.

Рассматривая проблему выбора конкретного вида функционала f(a, xt) из выражения (1.1) заметим, что в практике эконометрических исследований используется достаточно широкий круг функциональных зависимостей между переменными. Приведем некоторые, наиболее часто используемые, их виды:

1) линейная

yt =a0 +a1 х1t +...+an хnt +et, (1.2)

2) правая полулогарифмическая

yt=a0 +a1 lnx1t +...+an lnхnt +et, (1.3)

3) степенная

4) гиперболическая

yt =a0 +a1 /х1t +...+an /хnt+et, (1.5)

5) логарифмическая гиперболическая

lnyt =a0 +a1 /х1t +...+an /хnt+et, (1.6)

6) обратная линейная (функция Торнквиста)

1/yt=a0+a1 /х1t+...+an /хnt +et, (1.7)

7) функция с постоянной эластичностью замены

где l и r – также параметры функции.

8) экспоненциальная функция

где b1,..., bn – также параметры функции.

На практике могут встретиться и комбинации рассмотренных выше зависимостей. Например,

и т. п.

Здесь необходимо отметить, что большинство функций f(a, xt) с помощью определенного набора преобразований могут быть приведены к линейной форме (1.2). Например, если у и хi связаны зависимостью у~1/хi (выражение (1.5)), то, введя переменные ui=1/хi, получим выражение (1.2) с точностью до преобразования исходных факторов.

В практических исследованиях часто, используя преобразование ui=lnхi и z=lny, степенную модель (1.4) преобразуют к линейному виду, связывающему логарифмы переменных у и хi. Однако заметим, что в данном случае с точки зрения математики такое преобразование не совсем корректно из-за “аддитивности” ошибки в выражении (1.4). Вследствие этого значения коэффициентов линейной относительно логарифмов переменных модели нельзя в общем случае полагать равными соответствующим значениям степенного аналога.

На примере линейной эконометрической модели покажем еще одну возможную форму представления моделей такого типа – моделей, в которых отсутствует свободный коэффициент a0. В общем случае такая модель представляется в следующем виде:

Найдем взаимосвязи между переменными yt и , хit и и определим, чему равен коэффициент a0. Для этого просуммируем по индексу t правую и левую части модели (1.2). Получим

Поскольку что отражает свойство равенства нулю математического ожидания ошибки (M= ), то, разделив правые и левые части этого выражения на Т, получим

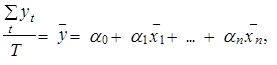
откуда следует, что

Вычтем a0 из уравнения (1.2). Получим для всех t

Из (1.12) непосредственно вытекает, что

Операция (1.13) определяет так называемые центрированные переменные и называется операцией центрирования. Отметим, что для центрированных переменных справедливы следующие очевидные соотношения:

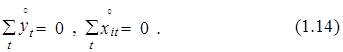
Использование центрированных переменных иногда значительно упрощает процедуры получения некоторых результатов, делает более наглядной их интерпретацию.

При этом следует помнить, что исходная информация для такой модели (вектор и матрица ) получается путем вычитания из каждого элемента каждого столбца соответствующего среднего (по столбцу) значения.

Как было отмечено выше, конкретный вид функциональной зависимости f(a, xt) может выражать какую-либо содержательную концепцию, отражающую предполагаемый характер взаимосвязей между процессами yt и хit, i=1, 2,..., n.

В основе использования степенной функции (1.4), например, обычно лежит концептуальное допущение о постоянстве частной эластичности выпуска у по каждому ресурсу (фактору) хi. Напомним, что частная эластичность в точке t показывает, на сколько процентов изменится зависимая переменная уt при изменении фактора хti на 1% при условии постоянства значений остальных факторов в этой точке. Частная эластичность определяется следующим выражением:

Подставим вместо уt в правую часть выражения (1.15) функцию . Учитывая, что 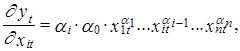получим

Эi = ai . (1.16)

Таким образом, коэффициент модели (1.4) ai сразу определяет значение эластичности у по фактору хi на всем интервале (1,Т).

Удобство экономической интерпретации параметров модели (1.4), относительная простота ее записи и послужили причиной ее широкого использования особенно в макроэкономических исследованиях.

Особую известность получили различные модификации двухфакторной функции Кобба-Дугласа

которые обычно применяется в макроэкономических исследованиях при анализе взаимосвязи между объемом полученного валового внутреннего продукта (y) и используемыми ресурсами (х1 – основные фонды и х2 – затраты живого труда). Между собой эти модификации, в основном, различаются ограничениями, накладываемыми на значения коэффициентов a1 и a2, а также способом выражения и содержательной интерпретацией коэффициента a0. Например, “классический” вариант функции (1.17) предполагает, что значения a1 и a2 удовлетворяют следующим ограничениям: a1+a2=1; a1, a2³0. В других вариантах этой функции дополнительно вводят сомножитель еrt, выражающий влияние на валовый продукт временного фактора, характеризующего научно-технический прогресс и т. п.

Функция (1.8) обычно используется в предположении о постоянстве эластичности замещения одного фактора другим. Например, если речь идет о замене фактора “труд”(L) фактором “капитал” (K), то значение коэффициента эластичности замещения показывает, на сколько процентов измениться капиталовооруженность (K/L) при изменении предельной нормы замещения труда капиталом (NKL =–dK /dL) на 1% при условии, что зависимая переменная не изменится. Значения всех других факторов при этом предполагаются также неизменными. В общем случае, эластичность замещения i-го фактора j-м определяется выражением:

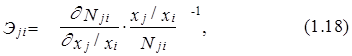
Предельная норма замещения i-го фактора j-м Nji показывает количество j-го фактора, которое требуется для замены одной единицы i-го фактора при сохранении постоянных уровня зависимой переменной и значений остальных независимых переменных.

Проводя расчеты по формуле (1.18) для функции (1.8), получим, что для всех i и j и для всех значений t=1,2,..., Т эластичность замещения прироста одного фактора соответствующим изменением другого является постоянной:

Во многих практических исследованиях столь строгие теоретические концепции, предварительные допущения о содержательных сторонах взаимодействия между явлениями отступают на второй план. Для них главным является построение уравнения, достаточно точно выражающего взаимосвязи, адекватные тенденциям изменений переменных у и хi, i=1, 2,...,n; на временном интервале (1,Т). Более того, часто именно “удачная” форма уравнения эконометрической модели кладется в основу разрабатываемой теоретической концепции, которая затем находит свое применение в последующем анализе. Очевидно, что наиболее “подходящая” форма обеспечивает наилучшее приближение теоретических (расчетных) значений = f(a, xt) к действительным значениям уt.

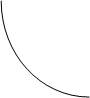
Обычно выбор такой формы осуществляется на основе графического анализа тенденций развития соответствующих процессов. Например, если переменная y и переменная хi изменялись во времени согласно графикам, представленным на рис. 1.1, то логично предположить, что у~1/хit .

Для графиков, представленных на рис. 1.2, характерной является логарифмическая зависимость уt ~lnхit.

В этих и во многих других случаях, как правило, в качестве функции f(a, xt), выражающей взаимосвязи между включенными в модель независимыми переменными хi, i=1, 2,..., n, выбирается либо линейная форма (1.2), либо степенная (1.4). Заметим, что значение частной эластичности y по фактору хi, рассчитанное на основе выражения (1.15) для функции (1.2) равно: