Качество оценок параметров эконометрических моделей

Эконометрическая модель считается построенной, когда определены значения оценок ее параметров. Исходными данными при этом являются наблюдаемые значения (измеренные уровни) зависимого показателя (переменной) уt  и независимых факторов хit, t=1,2,..., Т;  i=1,2,..., п. Таким образом, найденные количественные характеристики a0, a1,..., an  можно рассматривать как оценки истинных значений параметров модели a0, a1,..., an, в общем случае зависящие от исходных данных и применяемого метода оценивания.

Эти оценки являются случайными величинами. Их случайный характер можно интерпретировать следующим образом. Значения построенного функционала  f(a, xt)=, определенные при известном наборе оценок a0, a1,..., an, можно рассматривать как оценки, аппроксимирующие наблюдаемые значения зависимой переменной уt. Качество этой аппроксимации, а, следовательно, и качество параметров a0, a1,..., an  увязывается со свойствами и характеристиками случайной ошибки et=уt –. Таким образом, каждой выборочной последовательности ошибки et, t=1,2,..., Т;  ставится в соответствие “свой” набор параметров и наоборот. Это и позволяет говорить о каждом из таких наборов как о выборке из некоторого множества наборов оценок параметров a0, a1,..., an, соответствующей определенному методу оценивания.

В этой связи еще раз  отметим, что “истинным” значениям параметров a0, a1,..., aп  должен соответствовать и “истинный” ряд ошибки модели et, определенный как

et=уt –f (a, xt).                             (1.46)

Поскольку вектор истинных значений параметров a=(a0, a1,..., aп) неизвестен, то рассчитать значения et, t=1,2,..., Т; на основании выражения (1.46) на практике не представляется возможным. Однако при известных оценках коэффициентов a0, a1 ,..., an   можно определить “оценку” ошибки e, в качестве которой в данном случае выступают значения «фактической» ошибки  et=уt–f(a, xt), t=1,2,..., Т, полученные из выражения (1.46) при подстановке в функционал f оценок параметров. Ряд ошибки et  при этом также рассматривается как “выборочная ошибка”.

Полученную любым методом оценку ai  коэффициента эконометрической модели ai   можно рассматривать как выборочную случайную величину, представленную в виде суммы ее истинного значения ai  и случайной ошибки Dai , i=0,1,..., п.

ai=ai +Dai .                                  (1.47)

Из выражения (1.47) непосредственно вытекает, что о качестве оценки ai   в этом случае можно судить по свойствам ее ошибки Dai.

При этом, хотя истинное значение  ai  неизвестно, однако, как это будет показано далее, некоторые характеристики ошибки  Dai  и ее свойства обычно удается определить в процессе получения оценки ai .

В такой ситуации хорошее качество оценок параметров модели, полученных с использованием того или иного метода (о котором можно судить на основании характеристик качества их ошибок), является одним из важнейших условий построения “удачной” эконометрической модели. Напомним, что другим таким условием является правильное отображение основных закономерностей рассматриваемых процессов с учетом взаимосвязей между ними. Рассмотрим основные подходы к определению уровня качества оценок параметров эконометрических моделей более подробно.

Теория статистического оценивания качество оценок определяет по свойствам несмещенности, эффективности, асимптотической несмещенности и асимптотической эффективности, состоятельности и некоторым другим. Напомним, что оценка является несмещенной, если  истинное значение параметра можно рассматривать как ее математическое ожидание или, иначе, математическое ожидание ошибки оценки Dai  должно быть равно нулю:

M=ai, M=0.                               (1.48)

Оценка рассматривается как эффективная, если она характеризуется наименьшей дисперсией (дисперсия ошибки оценки минимальна) среди всех других аналогичных оценок, полученных различными методами, способами.

– дисперсия оценки, полученной с использованием j-го метода оценивания.

Часто свойство несмещенности выполняется лишь с некоторой степенью «приблизительности» при достаточно больших объемах выборочных данных (при большом числе измерений Т), в пределе при Т®¥. В этом случае говорят, что оценки являются асимптотически несмещенными. Иногда асимптотическая несмещенность рассматривается в “вероятностном” смысле, т. е. предполагается, что для произвольно малых положительных чисел x и h, в общем случае зависящих от Т, существует такой объем исходных данных Т0, что для всех Т>Т0 имеет место следующее неравенство:

или

где – вероятность события, заключенного в фигурные скобки. Выражение (1.50) означает, что предел по вероятности последовательности есть . Оценки, обладающие таки свойством, называют состоятельными. Свойство состоятельности в литературе обычно выражают символом

Обратим внимание на определенные различия, связанные с использованием в эконометрическом анализе свойств несмещенности, в одной стороны, и асимптотической несмещенности, состоятельности,  с другой. В эконометрических исследованиях значение Т  всегда конечно,  и часто не очень велико, что иногда определяется отсутствием необходимой информации. При конечных объемах выборки желательно выполнение для рассматриваемых характеристик свойств несмещенности и эффективности. Однако в ряде случаев доказать наличие у них таких свойств не представляется возможным, но можно показать, что они обладают свойствами асимптотической несмещенности, эффективности и состоятельности. Наличие таких асимптотических свойств у характеристик обычно в эконометрике является свидетельством более высокого их качества, по сравнению с другими альтернативными вариантами таких характеристик, которые этими свойствами не обладают.

Кроме того, “асимптотические”  свойства могут рассматриваться как преимущество “при прочих равных условиях”, в том смысле, что из двух оценок более предпочтительной является та из них, которая получена на основе большей по объему выборки (если по эффективности эти оценки не различимы)*.

Однако в этом случае следует проявлять определенную осторожность. Дело в том, что при конечных объемах выборки интуитивно предполагается, что, чем больше значение Т, тем ближе полученная оценка параметра к его истинному значению  и тем меньше ее ошибка. Но увеличение объема выборки ведет к уменьшению величины смещения только в том случае, если закономерности рассматриваемых процессов на “старом” и “добавленном” временных интервалах полностью идентичны (однородная выборка) и, таким образом, построенные на соответствующей этим интервалам информации модели будут малоразличимы.

 В эконометрике часто приходится сталкиваться с такой ситуацией, когда на отдельных временных участках закономерности процессов различаются. Это может быть вызвано, например, начавшимся воздействием на зависимую переменную уt   нового фактора, изменением характера взаимосвязей между рассматриваемыми переменными в связи с изменением их масштабов (действие диалектического закона перехода “количества” в “качество”) и по другим причинам. В этом случае увеличение числа измерений не ведет к автоматическому “росту качества” оценок параметров модели.

Важнейшими характеристиками, которые учитываются при изучении свойств  асимптотической несмещенности и состоятельности,  являются асимптотическое математическое ожидание и асимптотическая дисперсия.

Асимптотическое математическое ожидание параметра ai определяется как предел последовательности оценок его математических ожиданий, рассматриваемых при неограниченно возрастающем объеме исходных данных, т. е. количестве измерений Т:

где – оценка параметра, полученная при Т измерениях.

Асимптотическая дисперсия определяется как предел следующей величины:

где ai  – истинное значение этого параметра.

Выражение (1.53) сформировано с учетом того факта, что оценки , полученные на основе различных методов, могут иметь в пределе при Т®¥ одинаковую нулевую дисперсию. Например, дисперсия выборочного среднего равна /Т, а выборочной медианы – p/2Т и при Т®0 эти величины неразличимы. Вместе с тем, дисперсия случайной величины  равна  а у показателя дисперсия равна p/2, где – дисперсия генеральной совокупности, а  и  т – ее выборочное  среднее и выборочная медиана. Из сопоставления этих значений видно, что выборочное среднее более “качественная” (асимптотически эффективная) оценка, чем медиана. Таким образом, выражение (1.53) является более наглядным  при сравнении эффективности различных оценок параметров при увеличении Т.

Точно также рассмотренные свойства для конечных и бесконечных  выборок распространяются и на совокупность оценок параметров, представимых в виде вектора-строки a=(a0, a1,..., an)¢. Заметим, что в этом случае вместо дисперсии мы имеем дело с ковариационной матрицей этого вектора Cov(a), определяемой следующим выражением:

Cov(a) = M =

=   

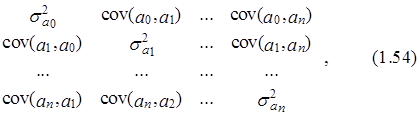
где Da¢  – вектор-строка ошибок параметров, Da¢=(Da0, Da1,..., Dan ), cov(ai, aj)– ковариация параметров ai  и aj; асимптотическое математическое ожидание вектора оценок параметров определяется согласно следующему выражению:

m( a)=( a(T ) ) =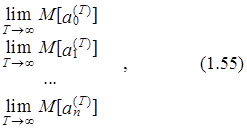 

а асимптотическая ковариационная матрица этих оценок – согласно выражению:

asyCov(a)=M{×¢}. (1.56)

Если оценка каждого из компонент вектора a состоятельна (в смысле выражения (1.50)), то состоятельным является и весь вектор. Тогда можно записать

plim(a(T ))=a.

Достаточным условием состоятельности оценки параметра модели является стремление к нулю величины математического ожидания и дисперсии ее ошибки (смещения) при возрастании объема выборки. Это условие следует из неравенства Чебышева, в свою очередь, вытекающего из следующих соотношений:

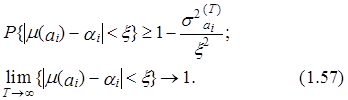
Заметим, что  где  – абсолютная величина ошибки оценки ai (Т ) в предположении, что Т®¥.

Таким образом, если и , т. е. оценка является асимптотически несмещенной,  то из (1.57) непосредственно вытекает, что, начиная с некоторого значения Т0  для всех Т>Т0 можно найти малое значение x, удовлетворяющее (1.57). Из этого следует, что plim(ai (Т ))=ai, и такая оценка является и состоятельной.

Обратное утверждение, вообще говоря неверно, т. е. состоятельные оценки не всегда являются асимптотически несмещенными. Однако при выполнении некоторых дополнительных условий установлено, что состоятельные оценки  обладают и свойствами асимптотической несмещенности. В частности, если оценка ai   несмещенная при конечном объеме выборки и состоятельная, то она обладает и свойством асимптотической несмещенности. Такой же вывод справедлив и в том случае, когда известно, что существует асимптотическое математическое ожидание состоятельной оценки и предел ее дисперсии  при Т®¥  равен  нулю, т. е.

Заметим также, что состоятельность является “более удобным” при анализе свойством, чем асимптотическая несмещенность, поскольку оно часто автоматически сохраняется при преобразованиях рассматриваемых переменных и некоторых операциях с ними. В частности, если f(a) – некоторая функция параметра a, то plim(f(a))=f(plim(a)). Например, plim(a2)=(plim(a)) 2.

Аналогичные свойства имеют место и при векторно-матричных вычислениях. Так, для произведения матриц, обратной матрицы справедливыми являются следующие соотношения:

plim(A×B))=(plimA)× plim(B);

(plimA–1)= (plimA)–1.

Различные методы определения значений параметров эконометрических моделей могут приводить к их оценкам, различающимся по своим количественным характеристикам. При этом  ухудшение свойств оценки иногда обусловливается тем, что исходные предпосылки применения того или иного метода не соответствуют свойствам рассматриваемого процесса.

Часто “необоснованность” предпосылок обусловлена тем обстоятельством, что в ходе анализа построенной модели не принимается во внимание “содержательная интерпретация” используемых данных. В связи с этим заметим, что обычно предположение о детерминированном характере независимых переменных хi, позволяет говорить о свойствах несмещенности и эффективности оценок параметров эконометрических моделей на конечных выборках (т. е. рассматривать проблемы наличия или отсутствия этих свойств у найденных оценок.

В том случае, если независимые переменные имеют случайный характер или при получении оценок параметров модели использовались так называемые “инструментальные” переменные – их заменители, то свойства полученных оценок уже имеют асимптотический характер. Иными словами, несмещенность и эффективность (если они имеют место) проявляются только на больших выборках.

В этой связи наиболее “популярными” методами оценки параметров линейных эконометрических моделей являются метод максимального правдоподобия и метод наименьших квадратов. Их “популярность” объясняется относительной простотой вычислений и высоким качеством получаемых оценок в смысле выполнения требований относительно их несмещенности, эффективности и состоятельности.