Модели цензурированных выборок

Напомним, что в  случае цензурирования зависимой переменной yt  вместо ее значений выше (или ниже) определенного уровня рассматривается сам этот  уровень.

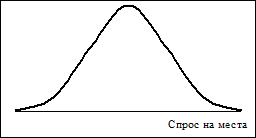
Например, если спрос на билеты существенно превышает предложение, то за уровень спроса принимается количество проданных билетов (цензурирование сверху). В этом случае распределение случайной величины может быть представлено в виде сочетания дискретного и непрерывного распределений (см. рис. 10.9).

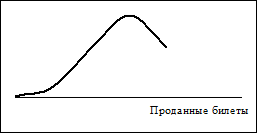
Рис. 10.9. Распределение, цензурированное “сверху”

Подходы к исследованию цензурированных и усеченных выборок очень похожи. Также обычно предполагают, что случайная переменная у имеет нормальное распределение.

Покажем, как изменятся математическое ожидание и дисперсия случайной переменной у, если выборка ее значений цензурируется снизу.

Введем в рассмотрение новую случайную переменную у*, такую, что

если у*£b, то у=b;

если у*>b, то у=у*,                         (10.153)

где b – точка цензурирования.

Если у*~N, то математическое ожидание и дисперсия цензурированной случайной величины y соответственно равны*

M=F×b+(1–F)×(m+s×l);                  (10.154) 

D=s2×(1–F)×,              (10.155)

где

F=F(b)=P(у*£ b)=F;                 (10.156)

 l=j/(1–F);                              (10.157)

 d=l2–l×b.                                (10.158)