Рассмотрим особенности метода максимального счета, применяемого наряду с методом максимального правдоподобия для оценки параметров модели бинарного выбора.
Этот метод использует критерий, представляющий собой максимум числа совпадений реальных и расчетных ответов, который критерий можно представить в следующем виде:
MaxaSb(a)=
(a¢xt)]* . (10.210)
Параметр b – это установленный квантиль; sgn(a¢xt) – знак числа a¢xt; zt=2yt –1 (zt =–1, если yt=0; zt=1, если yt=1). Если b=1, метод максимального счета выбирает оценку параметров a таким образом, чтобы максимизировать число раз, когда a¢xt имеет тот же знак, что и zt.
Метод по своей сути является полупараметрическим, поскольку он использует не параметры распределений, а их заменители.
Оценки параметров ai (i=1,2,…, n) определяются путем перебора возможных их сочетаний при заданном уровне точности (например, 0,0001) с учетом ограничения 
Так как метод максимального счета не предполагает вычисление функции правдоподобия, то невозможно определить и информационную матрицу для определения стандартных ошибок оценок. Чтобы получить представление об изменчивости оценок, обычно используется метод самонастройки (bootstapping). Он заключается в следующем. После вычиcления набора оценок коэффициентов aT из выборки делается К случайных подвыборок, содержащих по t наблюдений. Для каждой k-й подвыборок метод максимального счета дает свои оценки at(k). Тогда среднеквадратические отклонения можно оценить следующим образом:
Отметим еще раз, что элементы матрицы MSD не являются ковариациями соответствующих оценок, они лишь характеризуют их взаимную изменчивость.
Преимущество полупараметрических методов оценки параметров состоит в том, что при их использовании не возникают ошибки, связанные с неправильным выбором закона распределения погрешностей модели. С другой стороны, нет никаких гарантий, что полученные на их основе оценки будут лучше, чем «параметрические». Существенным недостатком полупараметрических методов является то, что они требуют очень большого количества вычислений для получения оценок параметров. Это выдвигает определенные ограничения в отношении максимального еоличества параметров модели и объема исходной информации. Сейчас метод максимального счета не используется для оценки более чем 15 коэффициентов на основе 1500-2000 наблюдений. Еще один недостаток этого подхода обусловлен невозможностью параллельного получения вместе с оценками параметров дополнительной информации, относящейся к характеристикам качества модели, точности оценок и т. п. Для содержательного анализа влияния факторов на зависимую переменную очень важны маржинальные эффекты, а на основе полупараметрических методов оценить их также не представляется возможным.
Как развитие метода максимального счета можно рассматривать, предложенный его авторами метод вторичного анализа результатов. Этот метод позволяет получить оценки математического ожидания переменной yt, в зависимости от величин, влияющих на нее факторов.
Рассмотрим основные положения этого метода. Пусть
Fa(zt )=M (10.212)
представляет собой гладкую функцию “отклика” yt на xt. Основываясь на векторе параметров оценок параметров a (полученном с помощью метода максимального счета), авторы предлагают построить Fa(zt) с помощью так называемого kernel-метода.
Для вектора оценок параметров a и известных значений независимых переменных xt (t=1,..., T) определим следующие значения:
zt=a¢xt, (10.213)
Для произвольного значения z*, принадлежащего области допустимых значений произведения a¢x, можно определить следующий набор весов (kernel-функций) wt (t=1,..., T):
где
(10.217)
и
Константа 
используется для стандартизации логистического распределения, которое применяется в kernel-функции; l – параметр сглаживания. Значения l должны быть досаточно велики, чтобы функция F(z*) была гладкой, использование маленьких, близких к нулю, значений l усиливает большую колебания функции. Хорошей теоретической основы для выбора l не существует, за исключением некоторых предположений, которые можно сделать на основе описательной статистики.
Функция F(z*) (в выражении (2.212)) определяется следующим образом:
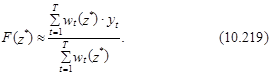
где – наблюдаемые значения уt, t=1,..., T.
Расчетные значения функции F(z*) при заданном наборе факторов хt обычно интерпретируются как математическое ожидание зависимой переменной yt (М).
Поможем написать любую работу на аналогичную тему