Оценка параметров распределений функциональных зависимостей случайных величин

Предположим, что между переменными у и х1, х2,..., xn существует функциональная связь

y=f(x),                                  (7.190)

где вектор x=(х1, х2,..., xn) является случайным с известным (нормальным) законом распределения x~N(M, Cov), и параметры M= и Cov (ковариационная матрица компонент вектора х) определены на основании временных рядов хit, i=1,2,..., n; t=1,2,... T.

Очевидно, что в этом случае переменная у также является случайной величиной. Ее закон распределения является асимптотически нормальным, а его параметры могут быть определены на основании разложения функции f(x) в ряд Тейлора в окрестности точки M. Ограничиваясь первым порядком разложения Тейлора, получим:

где  – значение функции f(x) в точке  и  –  значение производной в этой точке.

В силу того, что , получим:

Дисперсию переменной у определим следующим образом:

Из выражения (7.193) вытекает, что в точке  дисперсия переменной у может быть определена в предположении о независимости производных  и приростов на основании следующего выражения:

где  – математическое ожидание производной в точке ; Cov()– ковариационная матрица компонент вектора .

В том случае, когда компоненты вектора  независимы между собой, выражение (7.194) приобретает следующий вид:

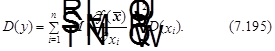
Используем выражения (7.194) и (7.195) для оценок параметров распределений некоторых комплексных (сложных) переменных, рассмотренных в разделе 7.3.

Дисперсия случайной величины SR, представляющая собой отношение (выражение (7.31)) на основании выражения (7.195) оценивается следующим образом:

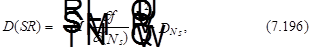
где  определена выражением (7.185), fºSR.

Поскольку

то, подставляя правые части выражений (7.185) и (7.197) в выражение (7.196), получим:

Выражение (7.198) в точности соответствует выражению (7.45).

На основании выражения (7.194) определим также параметры отношения двух дисперсий s12 и s22, которое представляет собой отношение VR(2)=s22/s12 (см. выражения (7.56)–(7.58)).

Из выражений (7.56), (7.57) и (7.192) непосредственно следует, что

Дисперсию этого отношения найдем как дисперсию функции

Такое преобразование целесообразно, поскольку случайные величины, стоящие в числители выражения (7.200) и его знаменателе, являются независимыми между собой. Это следует из того факта, что эффективная оценка q1 параметра q асимптотически некоррелирована с разностью q2–q1, где q2  – другая оценка этого параметра. Этот результат вытекает из следующего рассуждения. Если условие независимости q1 и разности q2–q1 не выполняется, то можно найти линейную комбинацию оценок q1  и q2–q1, которая будет более эффективной оценкой параметра q по сравнению с q1, что противоречит исходной информации об эффективности оценки q1.

В нашем случае s12 является эффективной оценкой дисперсии sy2. Тогда для нее можно записать при Т®¥ следующее равенство:

Откуда непосредственно следует, что

Подставляя в выражение (7.201) оценки D(s12) и D(s22) (см. выражения (7.189),(7.57) и (7.58)), получим:

Далее, дисперсию функции f(y), определенную выражением (7.200) с учетом независимости его числителя и знаменателя согласно формуле (7.195) представим в следующем виде:

С учетом того, что   а в силу равенства нулю математического ожидания числителя выражения (7.200), и, принимая во внимание результат (7.202), получим