Особенности систем взаимозависимых моделей

При формировании и построении эконометрических моделей в предыдущих разделах предполагалось, что между независимыми переменными х1t,..., хпt  и зависимой переменной уt  в каждый момент времени существует только односторонняя прямая взаимосвязь: хi ®у, i=1, 2,..., п.  В такой ситуации зависимая переменная уt  не оказывала никакого влияния на переменные, входившие в правую часть модели.

Это не означает, что переменные хit, i=1, 2,..., п, характеризовались как абсолютно независимые. Однако предопределяющие их значения причины, факторы не находились под воздействием явления, отражаемого переменной уt.

Таким образом, в тенденциях развития переменных хit   и уt  просматривалась как бы строгая очередность. Сначала в момент (период) t возникали явления, выражаемые независимыми в модели переменными хit, а затем под их влиянием формировалось явление, которое выражалось переменной уt .

В реальной жизни многие экономические и социальные явления развиваются, воздействуя друг на друга одновременно, так что в единичный период времени, обозначаемый индексом t, невозможно установить, какое из этих явлений первично, а какое вторично. В качестве типичного примера такой взаимосвязи обычно называют соотношение между спросом и предложением, характеризующееся в единичном интервале времени взаимным влиянием друг на друга цены и объема производства (потребления) товара при участии некоторого количества других факторов, которые можно считать независимыми. Простейший (и достаточно условный) вариант эконометрической модели, описывающей динамику этих переменных на равновесном рынке, можно представить в виде следующей системы, состоящей и двух уравнений:

Qt=a0+a1×Pt+e1t,

Pt=b0+b1×Qt+b2×It +e2t,                              (8.1)

где Pt  – средняя цена за единицу товара, зафиксированная на рынке в период t; Qt  – объем производства (предложения) в период t; It  –  средний уровень дохода потребителя в период t; a0, a1  и b0, b1, b2  – коэффициенты первого и второго уравнений соответственно; e1t и e2t – ошибки первого и второго уравнений соответственно.

Первое уравнение системы (8.1) показывает, что объем производства товара в период t зависит от сложившейся на него на рынке цены. Во втором уравнении уже уровень цены на товар ставится в зависимость от объема его предложения и дохода потребителей, величина которого в этой системе предполагается известной. Таким образом, переменная It  в системе (8.1) является единственной чисто независимой переменной, а переменные Pt  и Qt  являются взаимозависимыми, т. е. в одном уравнении одна переменная рассматривается как зависимая, а другая – выступает в качестве независимой. Во втором уравнении они меняются местами.

Вообще говоря, “одновременность влияния” различных переменных друг на друга в большинстве случаев можно рассматривать как одно из допущений модели, целесообразность введения которого вызывается, например, укрупнением временного интервала t. В реальности вряд ли можно обнаружить рынок, на котором равновесные цены и объемы товаров формировались бы одновременно. Обычно эти показатели изменяются в ходе работы рынка на основе попеременной корректировки одного из них с учетом известного значения другого. Производитель, реагируя на рыночные цены, выпускает определенное количество товара (продавец закупает товар у оптовика). С учетом нового объема предложения и покупательской способности населения на рынке формируется новая цена (корректируется цена на товар). Такая очередность во взаимовлиянии предложения товара и его цены  относительно непродолжительный период времени соответствует несколько другой модификации системы эконометрических уравнений, имеющей следующий вид:

                                      Qt=a0+a1×Pt–1+e1t,

Pt=b0+b1×Qt+b2×It +e2t,                             (8.2)

в которой взаимосвязи между взаимозависимыми переменными выражаются следующей последовательностью: Pt–1®Qt®Pt® Qt +1.

В системе (8.2) одновременные взаимосвязи между переменными Pt  и Qt  отсутствуют. Однако, если периоды будут укрупнены (например, дневные в недельные, месячные в квартальные и т. п.), то в рамках укрупненного периода уже возникают одновременные взаимосвязи между переменными Pt  и Qt. Использование в данной ситуации в качестве объясняющей переменной значения Pt–1  становится нецелесообразным, поскольку реакции покупателя и продавца проявляются уже в рамках одного и того же периода. В этом случае взаимосвязи между переменными Pt  и Qt  уже определяются системой (8.1). При этом, например, Pt  может рассматриваться как средняя цена за этот укрупненный период, а Qt   – как объем продаж (предложения). Разумеется, что при определении длины укрупненного периода большое значение имеет вид товара. Для товаров повседневного спроса уже неделю можно рассматривать в качестве такого периода, а для некоторых средств производства и годовой продолжительности может быть недостаточно.

В отношении ошибок системы (8.1) e1t и e2t  выдвинем традиционные предположения об отсутствии в ряду каждой из них явлений гетероскедастичности и автокорреляции:

В целях упрощения предварительных рассуждений предположим также, что временные ряды ошибок e1t и e2t  статистически независимы, т. е. cov(e1t, e2t)=0.

Посмотрим, сохраняется ли для системы (8.1) условие (2.23), выполнение которого позволяет получить несмещенные оценки коэффициентов модели a0, a1, b0, b1, b2   с использованием МНК.

Подставим во второе уравнение системы (8.1) значение Qt, выраженное через Pt. Получим

откуда следует, что

где –  коэффициенты новой модели и – новая случайная ошибка, являющаяся линейной комбинацией независимых ошибок e1t и e2t. В силу условия (8.3) несложно убедиться, что

Из выражения (8.4) следует, что в общем случае на зависимую переменную Pt  воздействует случайная ошибка иt, в которую входит ошибка первого уравнения e1t. Таким образом, переменные Pt    и e1t  нельзя считать независимыми и

Иными словами, входящие в первое уравнение независимая переменная и ошибка оказываются коррелированными, а, следовательно, и прямое использование МНК для получения оценок коэффициентов этого уравнения даст смещенные результаты. При этом из выражения (8.5) следует, что это смещение не может быть устранено увеличением объема выборки, поскольку  при всех значениях T.  Напомним, что величину смещения оценок a0  и a1, согласно выражению (2.9), можно оценить как            , где 

X =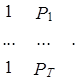    

Оценки со смещением, не устраняемым увеличением объема выборки, называют несостоятельными. Если такие оценки получены с использованием МНК, то часто употребляется термин “несостоятельный МНК”.

Аналогично можно показать, что во втором уравнении системы (8.1) переменная Qt   связана с ошибкой e2t  и применением обычного МНК и в этом случае ведет к смещенным оценкам параметров b0, b1   и b2.

Заметим далее, что, вообще говоря, уравнения системы (8.1) могли бы быть рассмотрены и по отдельности. Однако это не будет означать, что взаимосвязи между переменными, входящими в их правые части, и соответствующими ошибками исчезли. Эти взаимосвязи существуют вне зависимости от того, объединяются ли данные уравнения в систему. Они предопределены характером взаимоотношений в экономике между рассматриваемыми процессами, а не самим объединением их в систему. Просто в системе взаимосвязи между независимыми переменными и ошибкой становятся непосредственно очевидными, поскольку они могут получить количественную оценку.

Таким образом, системы взаимозависимых эконометрических моделей выражают через структурную форму взаимосвязей между явлениями их новое содержание, характеризующееся взаимным влиянием друг на друга некоторых зависимых и независимых переменных. В этой связи следует заметить, что можно строить отдельную модель этой системы для отдельно взятой зависимой переменной, но при этом следует иметь в виду, что если она, в свою очередь, в то же время влияет на какую-либо из независимых переменных, то использование МНК для получения оценок коэффициентов этой модели дает смещенные результаты.

Здесь следует отметить, что корреляционные взаимосвязи между эндогенными переменными и ошибками появляются и в том случае, когда некоторые из уравнений системы (8.1) имеют характер тождества. Рассмотрим, например, упрощенную модель агрегированного спроса в зависимости от величины дохода при балансовом ограничении на величину дохода:

Сt=b+a×It+et,

It=Сt+Zt,                                               (8.6)

где Сt  – потребительские расходы в период t, определяющие величину спроса; It  – размер дохода в период t; Zt    – потребительские расходы в период t; et  – ошибка модели, удовлетворяющая свойствам типа (8.3); b и a  – коэффициенты модели. Заметим, что во втором уравнении системы (8.6) отсутствует ошибка, и коэффициенты при объясняющих переменных строго предопределены балансовым соотношением. Они равны единице.

Подставив первое уравнение из (8.6) во второе, получим

Таким образом, коэффициент ковариации между переменными It  и et  в силу условий (8.3) оказывается отличным от нуля:

Вместе с тем следует отметить, что существует класс систем взаимозависимых эконометрических моделей, в которых эндогенные переменные и ошибки можно считать статистически независимыми. Это так называемые “рекурсивные системы”. Простейшим их примером можно считать систему (8.2).

В результате подстановки первого уравнения из (8.2) во второе получим

Pt=(b0+b1 ×a0)+b1×a1 ×Pt–1+b2×It +b1 ×e1t +e2t .             (8.8)

Из выражения (8.8) вытекает, что цена товара Pt   в период t, определяемая вторым уравнением, зависит от ошибки первого уравнения. Однако, поскольку при определении коэффициентов первого уравнения из (8.2) используется не значение Pt, а значение Pt–1, которое не связано с ошибкой et*, то использование МНК не приводит к смещению оценок коэффициентов a0  и a1.

С учетом этого факта коэффициенты каждой из эконометрических моделей, входящих в рекурсивную систему, могут быть оценены с использованием обычного МНК и полученные их оценки не будут смещенными.

Рассмотрим проблемы построения систем взаимозависимых эконометрических моделей более подробно, в том числе и с формальных позиций.