Оценивание параметров структурной формы на основе  двухшагового МНК с использованием инструментальных переменных

Двухшаговый МНК является одним из наиболее “популярных” методов оценки параметров моделей структурной формы. Причем обычно он используется в случае изолированного рассмотрения каждой из моделей системы. Рассмотрим особенности применения этого метода на примере первого уравнения структурной формы (8.9), которое представим в целях сокращения обозначений в следующем виде:

В матричной форме записи модель (8.49) для t=1,2,...,Т  может быть записана следующим образом:

 у1=Y1×a1+X1×b1+e1,                            (8.50)

где у1 – вектор значений зависимой в модели (8.49) переменной у1t, t=1,2,...,Т;

Y1 – матрица значений эндогенных переменных системы моделей, входящих в модель (8.49) в качестве независимых переменных,

Y1  =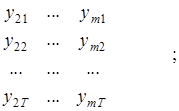      

 

X1  – матрица значений экзогенных факторов первого уравнения системы, являющихся чисто независимыми переменными. Она формируется с учетом параметра b0 традиционным способом на основе значений экзогенных факторов, входящих в первое уравнение;

a1=(a21,..., am1) – вектор-столбец коэффициентов при эндогенных переменных уi , i=2,..., m;

b1=(b01,..., ) – вектор-столбец коэффициентов при экзогенных переменных хj, j=0,..., n1.

Как и ранее, предполагается, что эндогенные переменные уi взаимосвязаны с ошибкой ei, а переменные хj  – нет. Вследствие наличия взаимосвязи независимых переменных и ошибки применение обычного МНК для определения параметров модели (8.50) дает смещенные оценки.

Основная идея использования двухшагового МНК для оценки коэффициентов модели (8.50) состоит в следующем.

1. На первом шаге конструируются новые значения зависимых переменных , таким образом, чтобы ряды уit   и были  в некотором смысле близки друг другу, но ряды  и ошибку ei  можно было бы считать независимыми,  i=2,..., m.

2. На втором шаге значения используются вместо значений уit при оценке коэффициентов модели (8.50) также с помощью обычного МНК. Иными словами, в этом случае матрицу  Y1  при  оценке  коэффициентов  предлагается  заменить  на матрицу  , которая имеет следующий вид:

Y1   =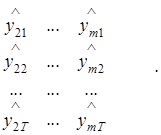       

При этом в литературных источниках при определении значений , i=2,..., m, обычно рекомендуется использовать соответствующие уравнения приведенной формы системы. В соответствии с этим данные значения определяются как расчетные значения зависимых переменных “классических” эконометрических моделей для моментов времени t=1,2,...,Т

при иitº0 (в соответствии с традиционным свойством ошибки M=0), так что

где, в свою очередь, оценки сij коэффициентов gij  находятся опять же с помощью обычного МНК на основании известного выражения

сi  =(X¢×X)–1 ×X¢×Yi ,                              (8.53)

где сi =(сi0 ,..., сik)¢, Yi=(yi1,..., yiT)¢, X – матрица значений независимых переменных, входящих в приведенную форму системы эконометрических уравнений. Ее размер равен Т´(k+1), где k – общее число независимых переменных системы. В то же время в каждом из ее структурных уравнений количество переменных, рассматриваемых как независимые, может быть меньше, чем k. Таким образом, п£ k. Заметим, что в качестве независимых переменных могут рассматриваться как чисто экзогенные факторы, так и эндогенные запаздывающие переменные, чьи значения уi,t-r   не могут быть связаны с ошибкой eit (из-за разницы во времени), где r – величина запаздывания (см. пример 8.3).

Несложно заметить, что переменные  являются некоторым вариантом инструментальных переменных, рассмотренных в разделе   3.3.  Вследствие этого многие проблемы оценивания параметров эконометрических моделей с использованием инструментальных переменных практически «автоматически» переносятся и на оценки коэффициентов структурной формы систем таких моделей. В частности, теория свидетельствует, что при выполнении обычных предположений относительно независимости  факторов и ошибки, гетероскедастичности и некоррелированности ошибки в пределе при Т®¥, и ряда других (см. главу 3), найденные с помощью подобной процедуры оценки коэффициентов, входящих в систему структурных уравнений (эконометрических моделей), являются состоятельными и что свойство состоятельности с точки зрения практики можно толковать как уменьшение смещения оценок с ростом числа наблюдений (длины рядов исходных данных). Более того, в этих условиях оценки имеют асимптотически нормальное распределение, что позволяет использовать при анализе качества построенных моделей параметрические критерии Стьюдента и Фишера.

Вместе с тем, в реальных эконометрических исследованиях, как правило, длина ряда исходных данных ограничена (т. е. зафиксирована конкретным значением Т). В такой ситуации уместен вопрос, начиная с какого количества наблюдений можно считать, что смещения оценок стали незначительными и их можно не принимать во внимание в дальнейшем анализе.

Ответа на этот вопрос теория не дает. Более того, результаты практических исследований часто свидетельствуют, что при относительно коротких временных рядах исходных данных смещенность оценок, полученных с помощью двухшагового МНК, может быть достаточно существенной, по крайней мере, сопоставимой со смещенностью оценок, полученных на основе обычного МНК.

Вместе с тем, свойство состоятельности оценок двухшагового МНК многими специалистами рассматривается как очевидное преимущество этого метода по сравнению с одношаговым МНК, и поэтому именно  процедуры двухшагового МНК обычно рекомендуются для построения структурных форм систем взаимозависимых эконометрических моделей в исследованиях реальных процессов.

Рассмотрим проблемы получения оценок коэффициентов уравнений структурной формы системы эконометрических моделей более подробно на примере модели (8.49).

Первый шаг.

На основании выражения

                                =X×(X¢×X)–1 ×X¢×Y1 ,                              (8.54)

определяется матрица расчетных значений эндогенных переменных

Выражение (8.54) учитывает, что уравнение (8.52), на основании которого рассчитываются значение переменной , в векторно-матричной форме принимает следующий вид:

                                                          = X×ci =X×(X¢×X)–1 ×X¢×уi ,

   

где   = ()¢ – вектор-столбец матрицы , ci=(ci0, ci1,…, cik)¢ – вектор-столбец коэффициентов уравнения (8.52). В результате для i=2,..., m на основе значений  формируется матрица .

Второй шаг.

Заметим, что матрица значений независимых переменных структурной формы модели (8.49) может быть представлена в виде объединения матриц Y1  и  Х1, т. е. , а вектор    коэффициентов – в виде объединения векторов a1  и b1, т. е.

  a1   

      b1      .

На втором шаге матрица Y1  заменяется на матрицу . Таким образом, оценки коэффициентов модели (8.49) согласно МНК определяются на основании следующего выражения:

                          = { ¢× }-1× ¢ × y1,        (8.55)

где y1  – вектор-столбец наблюдаемых значений переменной y1, состоящей из  Т компонент;

  – матрица значений “независимых” переменных модели (8.49) размера Т´(т+п).

      Матрица ¢ равна матрице   Y1 ¢

                                                               Х1¢   .

С учетом правил умножения матриц блочного типа окончательный вид выражения (8.55) может быть записан следующим образом:

                    a1                                     –1              × y1

                            =                                                                  ×                    .     (8.56)

                     b1                       Х1¢                Х1¢Х1                          Х1¢ × y1     

Заметим, что каждое расчетное значение эндогенной переменной на основании выражений (8.51) и (8.52) можно представить в следующем виде =уit –иit, где иit  – значение ошибки i-го уравнения приведенной формы в момент t, i=2,..., m. С использованием значений иit  сформируем матрицу U1  размера Т´(т–1).  Поскольку ошибки иit   по предположению по своим свойствам близки к процессу “белого шума” (обычное предположение МНК), то можно ожидать, что временные ряды и иit, как и ряды хjt   и иit,   будут статистически независимыми. С учетом этого матрица U1  удовлетворяет следующему равенству:

                                                                         ×U1 =0= Х1 ¢×U1 .                             (8.57)

                                                                                                                

Используя очевидные равенства =Y1–U1 и Х1¢×U1=0=U1¢×Х1  и представление матрицы  в форме (8.54), выражение (8.56) можно переписать в следующем виде:

a1            Y1¢Х×(Х¢×Х) -1×Х¢Y1           Y1¢Х1   –1         Y1¢Х ×(Х¢×Х) -1×Х¢×y1

      =                                                                                          ×

b1                            Х1¢Y1                               Х1¢Х1                                Х1¢ × y1                         .(8.58)

В выражении (8.58) учтено, что в соответствии с (8.57)

=(Y1 –U1) =Y1¢Х×(Х¢×Х) -1×Х¢Y1, а Х1=(Y1¢–U1¢)Х1=Y1¢Х1.

С учетом матрицы U1 выражение (8.50) можно записать в следующем виде:

                                                y1 = × a1  + Х1× b1 +( e1 + U1× b1).                    (8.59)

                                                                                                                                                                        

В целях упрощения записи обозначим матрицу через Z1, вектор (a1, b1)¢ – через d1. C учетом новых обозначений выражение (8.56) можно представить в традиционном виде:

d1 =(Z1¢×Z1)–1×Z1¢×y1

и ошибку этого вектора согласно выражениям (2.9), (8.50)  и (8.59) как

Dd1 =(Z1¢×Z1)–1×Z1¢× (e1 +U1×b1).                  (8.60)

Из условия (8.57) следует, что Z1¢×U1 =0. В силу этого выражение (8.60) приводится к следующему виду:

Dd1 = (Z1¢×Z1)–1×Z1¢× e1.                            

Таким образом, из выражения (8.60) следует, что вопросы определения факта смещения и его величины у оценок коэффициентов структурной формы каждого уравнения системы взаимозависимых эконометрических моделей сводятся к исследованию свойств произведения

                                                                                 Z1¢× e1        =     × e1

                                                                           Х1¢× e1  .                         (8.61)

В случае независимости (или отсутствия корреляции в пределе) у экзогенных переменных хjt, j=0,..., k; и ошибки e1t  можно ожидать, что M=0 и оценки вектора d1, полученные из выражения (8.56), окажутся несмещенными (состоятельными). В самом деле, независимость хjt, j=0,..., п; п £ k, входящих в структурную форму, и ошибки e1t непосредственно влечет за собой равенство         M=0.

В случае состоятельности в качестве исходной предпосылки  рассматривается равенство

 Х1¢× e1]=0.

Далее, поскольку матрица расчетных значений эндогенных переменных   выражается через полную матрицу значений всех экзогенных переменных Х и матрицу оценок  коэффициентов приведенной формы cij, i=2,..., m; j=0,..., k, которую обозначим через С, согласно следующему выражению:

                                                             

 = Х ×С,                                      (8.62)

то произведение × e1 можно представить в следующем виде:

                                                             

 × e1 = С¢× Х¢× e1  .                                      (8.62)

Заметим при этом, что из независимости переменных хп+1,..., хk  и ошибки e1  также должно следовать, что M=С¢×M=0. Однако этот теоретический вывод опровергается результатами практических исследований, которые свидетельствуют, что переход от фактических значений уit   к их расчетным значениям – инструментальным переменным  путем определения их значений с помощью выражения (8.52), не устраняет смещения в условиях малых выборок (при небольшом количестве измерений).

Вместе с тем, свойство состоятельности оценок коэффициентов структурной формы системы взаимозависимых эконометрических моделей при состоятельности оценок коэффициентов ее приведенной формы сохраняется.

На основании выражения (8.61) может быть получена оценка ковариационной матрицы параметров соответствующего уравнения структурной формы системы  эконометрических моделей. Напомним, что в соответствии с выражением (2.14) для первого уравнения эта матрица при отсутствии в ряду e1  автокорреляционных связей и наличии свойства гомоскедастичности имеет следующий вид:

Cov(d)=M=se2  × (Z1¢×Z1)–1 =

                                                                                                                  

=se2  ×      ×         × Х1         –1

                                                  Х1¢ ×        Х1¢ × Х1               .                (8.64)

                                                                                                                                                     

  Выражая значения элементов матрицы  через значения экзогенных и эндогенных переменных структурной формы системы (см. выражение (8.58)), Cov(d) можно также представить в следующем виде:

Cov(d) =se2  ×    Y1¢ × Х×(Х¢×Х) -1×Х¢ Y1           Y1¢ × Х1        –1

                                        Х1¢ × Y1                       Х1¢ × Х1               .               (8.65)

Дисперсия ошибки se2   оценивается согласно выражению      (2.19) следующим образом:

se2  =( y1 – Y1 ×a1  – Х1 ×b1)¢ × (y1 – Y1 ×a1  – Х1 ×b1)/(Т– т – п).        (8.66)

Матрица Cov(d), определенная на основании выражений (8.64) и (8.65) является состоятельной оценкой ковариационной матрицы параметров структурной формы системы взаимозависимых эконометрических моделей, в том смысле, что при достаточно большом количестве измерений Т вероятность значительного отклонения ее элементов от истинных значений стремится к нулю.

В заключение данного раздела приведем варианты уравнений отдельных моделей системы взаимозависимых моделей (8.34) (пример 8.3), полученные с использованием обычного и двухшагового МНК.

Уравнения получены для ФРГ с использованием исходных данных за период 1960-1977 гг.

Уравнение 1.

(1 МНК) у1t  = 23,10 + 0,31 у4t + 0,51 у1,t- 1 + e1t ;

(2 МНК) у1t  = 22,81 + 0,30 у4t + 0,53 у1,t- 1 + e1t  .

Уравнение 2.

(1 МНК) у2t  = 10,72 + 0,0004 у4t + 0,79 х2,t- 1 + e2t ;

(2 МНК) у2t  = –16,84 – 0,1392 у4t + 1,43 х2,t- 1 + e2t  .

Уравнение 3.

(1 МНК) у3t  = – 29,72 + 0,17 у4t + 0,63 у3,t- 1 + e3t ;

(2 МНК) у3t  = – 22,27 + 0,13 у4t + 0,71 у3,t- 1 + e3t  .

Представленные варианты уравнений свидетельствуют о различии (порой значительном, как в случае второй модели, описывающей динамику инвестиций) между значениями коэффициентов отдельных моделей системы (8.34), полученных на основе обычного и двухшагового МНК. При этом, вообще говоря, при использованном для построения этих моделей количестве измерений (Т=18) нельзя сказать, что результаты, полученные на основе двухшагового МНК лучше, чем аналогичные результаты, основанные на обычном МНК.

Первые и третьи пары уравнений свидетельствует о наличии различий в оценках их коэффициентов. Если ориентироваться на “теорию”, двухшагового МНК, то данные результаты можно интерпретировать как эмпирическое доказательство того, что этот метод действительно “корректирует” соответствующие оценки, полученные на основе обычного МНК. Однако остается вопрос: в какой степени смещение оценок устранено?  Достаточно ли для этого всего 18 измерений, когда теория утверждает, что его “полное” устранение имеет место при Т®¥?

Вторая пара уравнений вообще свидетельствует о принципиальных различиях результатов, полученных с использованием обычного и двухшагового МНК. На это указывают изменения знаков коэффициентов при однотипных переменных. В частности, двухшаговый МНК дает основание считать, что с увеличением национального дохода происходит более значительное изменение структуры инвестиций в сторону увеличения доли частного капитала, по сравнению с результатами обычного МНК. Увеличение национального дохода ведет даже к снижению капитальных вложений в экономику. Иными словами, результаты, полученные на основе двухшагового МНК, заставляют переосмыслить экономические предпосылки модели (8.34).

Укажем еще на один вычислительный аспект, который может воспрепятствовать получению «хороших» оценок коэффициентов структурной формы системы эконометрических моделей с использованием двухшагового МНК и инструментальных переменных, значения которых определяются на основе приведенной формы. Обратим внимание на то, что согласно выражениям (8.52) и (8.54) значения  инструментальных  переменных  , образующие  соответcтвующие столбцы матрицы , определяются как линейные комбинации одного и того же множества переменных хjt, j=1,2,..., k, значения которых являются элементами матрицы Х2.

В такой ситуации, во-первых, при совпадении тенденций хотя бы у двух эндогенных переменных уlt   и уrt,  значения которых образуют соответствующие столбцы матрицы Y1, возникает угроза линейной зависимости аналогичных столбцов

матрицы . Такая угроза особенно реальна, если число независимых переменных хj   невелико. Во-вторых, если количество экзогенных переменных в каком-либо уравнении системы приближается к общему числу таких переменных во всей системе и, таким образом, матрицы Х1  и Х2  совпадают  почти  или полностью, то можно ожидать, что зависимыми окажутся столбцы  и Х1.

Вследствие этого, матрица

                                                              Y1¢        Y1¢Х1   

                                         Х1¢                Х1¢Х1    

из выражения (8.56) окажется плохо обратимой, что повлечет за собой снижение точности оценок коэффициентов структурной формы рассматриваемого уравнения системы эконометрических моделей.

На наш взгляд, избежать подобных трудностей можно путем формирования значений инструментальных переменных   не на основе приведенной формы системы эконометрических моделей, а другими альтернативными путями, способами. В самом деле, нашей целью является формирование ряда (в случае первого уравнения системы i=2,..., m), тенденции которого совпадают с тенденциями соответствующей экзогенной переменной уit, но при этом случайные флюктуации ряда уit, взаимосвязанные с ошибкой eit  не должны учитываться.

Этого следует добиваться без использования уравнений приведенной формы. Например, инструментальные переменные можно сформировать как линейные комбинации каких-либо факторов, не включенных в систему взаимозависимых эконометрических моделей, в частности, как функции времени. Иными словами, в этом случае для получения их значений следовало бы вместо уравнений (8.52) использовать зависимости типа:

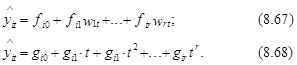
Заслуживает внимания предложение использовать для этой же цели зависимости авторегрессионного типа

построить которые можно, предварительно приведя исходный ряд уit   к стационарному и после построения подходящей модели авторегрессии для стационарного процесса выполнив обратное преобразование (см. главу VI).

При таких способах построения инструментальных переменных будут обеспечены все условия реализации двухшагового МНК: ошибка eit  не будет  связана с эндогенными переменными  и столбцы матрицы  окажутся менее зависимыми между собой и со столбцами матрицы Х1.

Существуют и другие подходы к формированию инструментальных переменных, реализация которых позволяет получить невырожденную матрицу значений факторов структурной формы уравнений, входящих в систему эконометрических моделей. Например, инструментальные переменные предлагается формировать на основе метода главных компонент, которые, в свою очередь, определяются на основании переменных, образующих матрицу Х2. Хотя и в этом случае, угроза необратимости матрицы остается.

Здесь следует иметь в виду, что разговор о преимуществах и недостатках одного метода оценивания коэффициентов структурной формы эконометрических моделей по сравнению с другим можно вести, лишь опираясь на статистику результатов использования этих методов при вполне определенных свойствах исследуемых процессов. На практике трудно подобрать достаточное количество реальных процессов, обладающих схожими свойствами, с тем, чтобы по результатам построенных для них моделей получить обоснованные выводы об эффективности каждого из методов. Вследствие этого для обоснования их эффективности часто используются результаты статистических экспериментов на основе метода Монте-Карло. Этот метод позволяет сформировать множество реализаций процесса, удовлетворяющего тем или иным статистическим свойствам (в нашем случае к ним относятся закон распределения ошибки, ее корреляция с переменными из правой части уравнений системы, корреляция ошибок различных уравнений и т. п.). Затем для таких реализаций с использованием того или иного метода строятся соответствующие модели, свойства оценок которых затем сопоставляются и между собой, и с предположениями, положенными в основу метода Монте-Карло.

Подобные эксперименты, проведенные в достаточном количестве, дают информацию об эффективности каждого из методов на основе сопоставления частот “положительных” и “отрицательных” результатов их использования при построении моделей. Конечно, такая информация не гарантирует эффективность использования метода в решении конкретной практической задачи. Но вместе с тем, общие выводы по результатам таких экспериментов представляются достаточно аргументироваными.

Результаты таких экспериментов свидетельствуют, что обычный МНК в случае конечных выборок дает большую величину смещения в оценках коэффициентов структурной формы отдельной эконометрической модели по сравнению с другими методами (двухшаговым МНК, ММП и некоторые другие). При этом с ростом объема выборки величина смещения и у обычного МНК также уменьшается. Отметим также, что в условиях мультиколлинеарности переменных правой части модели смещения оценок, полученных с помощью обычного МНК и других методов, являются сопоставимыми по величине. В целом же, у всех методов наблюдается отрицательная реакция смещения на эффект мультиколлинеарности данных, в том смысле, что с ростом степени мультиколлинеарности смещение оценок увеличивается. Однако у обычного МНК это увеличение происходит намного медленнее, чем у других методов.

Вместе с тем, результаты некоторых экспериментов также свидетельствуют, что обычный МНК по сравнению с альтернативными методами дает оценки, характеризующиеся меньшей дисперсией. Возможно, что этот эффект объясняется в ряде случаев коррелированностью ошибок различных моделей системы, которая при использовании двухшагового МНК и алгебраического метода,  основанного на построении превиденной формы системы, ведет к увеличению дисперсии оценок коэффициентов структурной формы моделей.

В таких случаях, когда имеет место (предполагается) корреляция между ошибками различных моделей, входящих в систему, предполагается, рекомендуется использовать трехшаговый МНК.