Эконометрические модели с эволюционными изменениями коэффициентов

Модель с эволюционными изменениями коэффициентов в общем случае имеет следующий вид:

где ai(t), i=0,..., n – оценки коэффициентов модели, меняющиеся во времени под влиянием каких-либо факторов, условий.

Иными словами, предполагается, что значения оценок коэффициента ai, рассматриваемые в различные моменты времени, например, t и t+1, могут различаться между собой, т. е. ai(t)¹ai(t+1).

Заметим, что в общем случае выражение (9.37) можно интерпретировать как модель (п+1)×Т  коэффициентами, поскольку в каждый момент t=1,2,..., Т значение ai(t) представляет собой как бы оценку “самостоятельного” коэффициента. Очевидно, что тогда определить весь набор значений ai(t), i=0,..., n, t=1,2,..., Т на основании Т независимых уравнений типа (9.37) не представляется возможным.

Обойти это ограничение возможно путем учета некоторых предварительных предположений относительно закономерностей изменения коэффициентов модели (9.37). В качестве такого предположения может быть рассмотрена гипотеза об определенном характере зависимости коэффициента ai(t) от некоторого набора факторов z1,..., zk, времени t и т. п. При этом обычно эти факторы являются внешними по отношению к модели переменными. Предположим, например, что коэффициентов ai(t), i=0,..., n, являются линейными функциями от одного внешнего фактора z и ошибки аппроксимации uit, происхождение которой будет пояснено ниже:

где bi0  и bi1 – неизвестные коэффициенты такой зависимости; zt  – известные значения фактора z  в моменты времени t=1, 2,..., T.

Подставим выражение (9.38) в модель (9.37). В результате получим:

Несложно заметить, что модель (9.39) отличается от модели (9.37) дополнительными слагаемыми, появившимися в правой ее части: и ошибкой  где хitº1, t=1,2,... Обозначив zt  как хп+1,t,   zt×х1t   как хп+2,t,..., zt×хпt     как х2п+1,t, получим традиционное выражение линейной эконометрической модели:

где  коэффициенты моделей (9.40) и (9.39) связаны следующими соотношениями:

Несложно заметить, что для модели (9.40) матрица значений факторов Х имеет следующий вид:

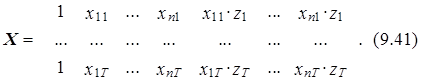
При известных значениях факторов х1t,..., хпt, zt, элементы этой матрицы определяются однозначно. В этом случае оценки коэффициентов модели (9.40) могут быть найдены с использованием рассмотренных в главах 2–4 методов с учетом свойств ошибки этой модели, например, с помощью обычного МНК при вполне естественном предположении о независимости ошибок  et, u0t,..., unt  между собой и со значениями независимых факторов xit. Обратим также внимание на эффект роста дисперсии ошибки при переходе от модели (9.37) к модели (9.39). Дисперсия последней модели при независимых ошибках определяется согласно следующему выражению:

где – дисперсия ошибки i-го уравнения (9.38),

Основной проблемой при оценке коэффициентов модели (9.40) является обоснование зависимостей, описывающих закономерности изменчивости коэффициентов ai(t), i=0,..., n. Дело в том, что априорно, используя только информацию, выраженную значениями переменных уt, х1t,..., хпt  и, может быть zjt, j=1,2,...,k; определить вид этих зависимостей не представляется возможным. Это связано с тем, что тенденции, закономерности изменчивости оценок коэффициентов ai(t) могут быть выявлены только после вычислительных экспериментов. На практике решение этой проблемы достигается путем последовательно перебора различных возможных вариантов этих зависимостей, по возможности используя для их сокращения, так называемый динамический подход. Его суть состоит в следующем.

Интервал t=(1, Т) разбивают на ряд частей, возможно пересекающихся. На каждой из них определяются оценки коэффициентов эконометрической модели классического типа, т. е. эти оценки предполагаются постоянными для каждой из рассматриваемых частей интервала. Таким образом, формируются ряды этих оценок

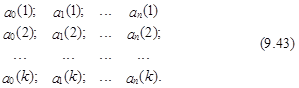
где ai(j) – значение оценки i-го коэффициента на j-й части интервала t=(1, Т).

Анализируя, тенденции изменения рядов ai(j), можно попытаться установить варианты возможных изменений рассматриваемых коэффициентов и обосновать наиболее подходящие для их описания зависимости. Далее, сравнивая характеристики качества построенных эконометрических моделей (дисперсии, коэффициенты детерминации, множественной корреляции), соответствующие этим вариантам, можно определить наиболее приемлемую среди них.

В некоторых случаях варианты зависимостей ai(t) могут быть сформированы на основе предварительно выдвигаемых гипотез. Например, гипотезу о стабилизации коэффициента ai во времени можно отобразить в виде следующего уравнения:

ai(t)= bi0+ bi1 /t,                                 (9.44)

где t – выражает переменную, влияющую на величину коэффициента ai.

Обозначив, z=1/t, получим, что при таком предположении матрица значений исходных факторов Х определена выражением (9.41).

Несложно заметить, что при известных зависимостях переменных коэффициентов ai(z, t) эконометрической модели, задача их оценивания в отсутствие каких-либо эффектов, вызванных плохой обратимостью матрицы (X¢×X), гетероскедастичностью или автокорреляционной зависимостью ошибки модели и т. п.,  может осложняться лишь из-за уменьшения числа степеней свободы, обусловленного ростом количества независимых переменных.

* Приведем типичный пример результатов анализа факторов, повлиявших на изменение цен на ряд товаров, реализуемых на крупнейших финансовых рынках мира (Элина Шкурупий. Китайцы обрушили серебрянный рынок. Известия, 29 февраля 2000 г., № 38, с.12): “Цены на серебро начали падать после сообщения о резком увеличении биржевых запасов наличного металла на складах СОМЕХ. Также на понижение сыграли слухи о возможном поступлении в продажу большой партии китайского серебра и о скором возобновлении работ на серебряных рудниках компании Penoles,  крупнейшего мексиканского производителя этого металла...

 После заявления министра нефти Саудовской Аравии о том, что его страна постарается не допустить увеличения нефтедобычи и после окончания срока действи нынешних квот, мировые цены на нефть в очередной раз пошли вверх...”

Благоприятный метеопрогноз для большей части зерносеящих регионов США привел к падению цен на пшеницу, кукурузу и сою-бобы и т.п.

* Напомним, что в соответствии с обычными для эконометрики предположениями значения Yt, qt, Rt, Qt; t=1,2, ... рассматриваются как реализации соответствующих случайных процессов, и для каждого момента времени эти значения рассматриваются как случайные величины.

* Ее основные положения вытекают из результатов работы Liber de Ludo Aleae (The Book of Games of Chance), опубликованной в 1565 г. итальянским математиком Джироламо Кардано.

* 1.Bachelier I., 1900; “Theory of Speculation” in Cootner,P.(ed). The Random Character of Stock Market Prices, pp.17-78, Massachusetts Institute of Technology Press, Cambrige, MA, 1964, Reprint.

2.Einstein, А. 1905. “Über die von der molekular-kinetischen Theorie der Wärme geforderte Bewegung von der in ruhenden Flüssigkeiten suspendierten Teilchen”, Annalen der Physik, 17; 549-560.

** ГСБ-1 с распределениями приростов, отличными от нормального, рассмотрена в работе Fama,E.F.(1965) “The behaviour of stock market prices”, Journal of Business, 38,  pp.34-105.

* Granger,C.W.J. and O. Morgenstern (1970). Predictability of Stock market Prices (Heath, Lexington, Massachusetts).

** В более общем случае m=mt   и mt =f(a, z) –  детерминированная составляющая процесса изменения цены, выраженная уравнением с коэффициентами a и аргументами, заданными вектором z.

*Напомним, что в силу независимости et–i  и et–j, i¹j, i, j=1,2, M=0.

* Cowles , A., Jones, H. “Some A Posteriori Probabilities in Stok Market Action”. Econometrica, 5, 1937.pp.280-294.

* Выражение (7.76) может быть получено с учетом того, что при t=1

* Выражения (7.97)-(7.100) можно получить, например, используя метод максимального правдоподобия для оценки параметров модели (7.25).

* Напомним, что процесс строгого белого шума предполагает независимость между моментами переменных ut  и ut-i  любых порядков, т.е.  . В нашем случае достаточно, чтобы это условие выполнялось для  k£4. Отметим также, что существуют классы моделей с изменяющейся вариацией, которые используют менее строгие предположения в отношении переменной ut  . В частности, некоторые из них допускают ненулевые автокорреляционные связи между квадратами ut2  и ut-i 2 (случай белого шума) или даже между значениями ut  и ut-i  (случай стационарного процесса).

* Заметим, что примером такого рода модели может быть и модель авторегрессионного типа с меняющимся условным математическим ожиданием:

в этом случае условная вариация значения yt  определяется следующим выражением:

где Mt–1 – математическое ожидание, определяемое в момент t–1, т. е. на основе информации, относящейся к этому моменту.

Далее, в предположении, что квадраты ошибок связаны моделью авторегрессии k-го порядка получим:

где ai  – коэффициенты модели, i=0, 1,..., k; nt   – ошибка.

Если значения коэффициентов ai, i>0, равны нулю, то рассматриваемая модель имеет постоянную условную дисперсию ошибки. Если a1¹0 и ai =0, i>1, то et   может быть определена выражением аналогичным (7.119), т. е. как

* Процесс, определенный выражением (7.120) в предположении, что переменная vt   не зависит от уровня цен Yt, Yt–1,... в литературе иногда называют процессом-произведением (“product-process”).

*

* Напомним, что пределы соответствуют доверительной вероятности р*=0,95 для стандартизованной случайной величины.

* Ошибка et   формируется позже, чем значение Pt–1, поэтому связь между этими переменными отсутствует.

* Здесь термин “равноправие” взят в кавычки с учетом того, что в моделях иногда используются весовые коэффициенты, определяющие различия в важности информации, содержащейся в разных строках матрицы Х и элементах уt, при определении значений коэффициентов (см. раздел 3.2). Однако этот вариант модели предполагает возможность изменения коэффициентов во времени.

* Рассматриваются фактически значения ошибки.

* Согласно процедуре (4.1)–(4.14) вектор оценок коэффициентов модели по t измерениям определяется на основании следующей последовательности расчетов:

* Ее значение определяется с использованием теории статистик Колмогорова-Смирнова.

* Эти точки могут быть определены с использованием какого-либо из рассмотренных в разделе 9.2 тестов.