Как выполняется сравнительный анализ моделей?

В эконометрике широко используются методы статистики. Чтобы дать количественное описание взаимосвязей между переменными, в эконометрике используются прежде всего методы регрессии и корреляции.

В зависимости от количества факторов, включенных в уравнение регрессии, различают простую (парную) и множественную регрессию.

 Простая регрессия представляет собой регрессию между двумя переменными  -   и  , то есть модель вида ,  где  - зависимая переменная (результативный признак);  - независимая, или объясняющая, переменная (признак-фактор).

Множественная регрессия представляет собой регрессию признака с двумя и большим числом факторов, т. е. модель вида .

Любое эконометрическое исследование начинается со спецификации модели, то есть с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между факторами.

Прежде всего из круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Иногда приходиться переходить от парной регрессии к множественной (если в процессе работы с моделью выявляются влияния на результативный признак не учтенных факторов).

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина  складывается из двух слагаемых: , где

 - фактическое значение результативного признака;

 - теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи  и , то есть из уравнения регрессии;

 - случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.

Случайная величина  называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами:

1)                графическим;

2)                аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

3)                экспериментальным.

Основные виды функций, используемых для построения модели регрессии: , , , , , .

Графический метод выбор вида математической функции  основывается на анализе расположения точек на корреляционном поле.

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии , рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии , то фактические значения результативного признака совпадают с теоретическими , т.е. они полностью обусловлены влиянием фактора . В этом случае остаточная дисперсия .

В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих, не учитываемых в уравнении регрессии, факторов. Иными словами, имеют место отклонения фактических данных от теоретических . Величина этих отклонений и лежит в основе расчета остаточной дисперсии:

         .

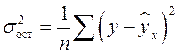Чем меньше величина остаточной дисперсии, тем меньше влияние не учитываемых в уравнении регрессии факторов и тем лучше уравнение регрессии подходит к исходным данным.

Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной . Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при  должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени , то требуется объем информации уже не менее 14 наблюдений.