Особенность связей в экономике и социальной сфере состоит в том, что их закономерный характер проявляется лишь в массе явлений – в среднем по совокупности. Такого рода связи называют статистическими. Они проявляются в том, что при изменении значения фактора изменяется значение результативного признака.
Корреляционная связь – частный случай статистической связи, при котором разным значениям переменной соответствуют разные средние значения другой переменной.
Если изучается связь между двумя признаками, то это парная корреляция. Если изучается связь между многими признаками – множественная корреляция.
Отклонения от средних по одной и другой переменным лежат в основе измерения корреляционной связи. В случае линейной связи ее теснота измеряется с помощью коэффициента парной корреляции:
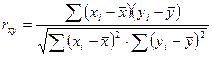или, можно показать, что 
.
Коэффициент парной корреляции измеряется от -1 (случай полной обратной связи) до 1 (случай полной прямой связи). Чем ближе значение 
к единице, тем теснее связь, чем ближе к нулю, тем слабее связь.
Для измерения не только линейных, но и нелинейных связей используется коэффициент детерминации, он равен квадрату коэффициента корреляции.
Математическое описание зависимости в среднем изменений результативного признака от факторных признаков называется уравнением регрессии.
В зависимости от количества факторов, включенных в уравнение регрессии, различают простую (парную) и множественную регрессию.
Простая регрессия представляет собой регрессию между двумя переменными - 
и 
, то есть модель вида 
, где - зависимая переменная (результативный признак); - независимая, или объясняющая, переменная (признак-фактор).
Множественная регрессия представляет собой регрессию признака с двумя и большим числом факторов, т. е. модель вида 
.
Поможем написать любую работу на аналогичную тему