Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например
– полиномы различных степеней – 
, 
;
– равносторонняя гипербола – 
;
– полулогарифмическая функция – 
.
2. Регрессии, нелинейные по оцениваемым параметрам, например
– степенная – 
;
– показательная – 
;
– экспоненциальная – 
.
Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции.
Парабола второй степени приводится к линейному виду с помощью замены: 
. В результате приходим к двухфакторному уравнению 
, оценка параметров которого при помощи МНК, как будет показано в параграфе 2.2 приводит к системе следующих нормальных уравнений:
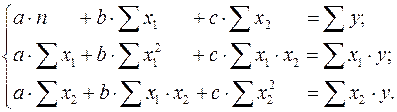
А после обратной замены переменных получим
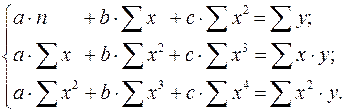(1)
Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую.
Равносторонняя гипербола 
может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы (например, кривая А.В. Филлипса), расходов на непродовольственные товары от доходов или общей суммы расходов (например, кривые Э. Энгеля) и в других случаях. Гипербола приводится к линейному уравнению простой заменой: 
. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
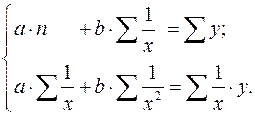(2)
Аналогичным образом приводятся к линейному виду зависимости 
, 
и другие.
Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся).
К внутренне линейным моделям относятся, например, степенная функция – 
, показательная – 
, экспоненциальная – 
, логистическая –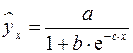 
, обратная – 
.
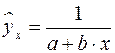К внутренне нелинейным моделям можно, например, отнести следующие модели: 
, 
.
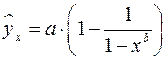Среди нелинейных моделей наиболее часто используется степенная функция 
, которая приводится к линейному виду логарифмированием:
;
;
,
где 
. Т.е. МНК мы применяем для преобразованных данных:
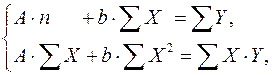
а затем потенцированием находим искомое уравнение.
Поможем написать любую работу на аналогичную тему