Характеристики степени тесноты связи в нелинейном случае в модели множественной регрессии.

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т. е. оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции: 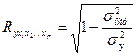, где  - общая дисперсия результативного признака;

   - остаточная дисперсия для уравнения .

Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:  ().

При правильном включении факторов в регрессионную модель величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.

Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

.                                                 

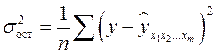Можно пользоваться следующей формулой индекса множественной детерминации:

         .                     

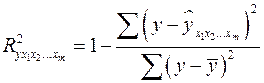При линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции: 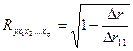, где  - определитель матрицы парных коэффициентов корреляции; - определитель матрицы коэффициентов парной корреляции.

Для уравнения  определитель матрицы коэффициентов парной корреляции примет вид:     

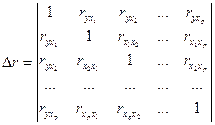
Определитель более низкого порядка остается, когда вычеркиваются из матрицы коэффициентов парной корреляции первый столбец и первая строка, что и соответствует матрице парной корреляции между факторами:

.

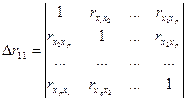Величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.

Индекс множественной корреляции равен совокупному коэффициенту корреляции не только при линейной зависимости рассматриваемых признаков. Тождественность этих показателей, как и в парной регрессии, имеет место и для криволинейной зависимости нелинейной по переменным.