Электронный газ в металлах

Валентные электроны в большинстве металлов свободно перемещаются. Они представляют собой почти идеальный квантовый Ферми-газ. Несмотря на их заряженность, электростатическое взаимодействие между электронами и ионами в значительной степени компенсируется. В результате кинетическая энергия электронов оказывается значительно больше потенциальной. Уровни энергии электронов в металле могут быть получены в результате решения стационарного уравнения Шредингера.

Рассмотрим электронный газ при абсолютном нуле Т = 0 (полностью вырожденный Ферми-газ). Электроны будут распределены в таком газе таким образом, чтобы полная энергия газа имела минимально возможное значение. Так как (согласно принципу Паули) в каждом квантовом состоянии может находится не более одного электрона, то электроны заполнят все состояния с энергией от наименьшей (равной нулю) до некоторой наибольшей, величина которой определяется числом электронов в газе. С учетом двукратного спинового вырождения уровней, число квантовых состояний электронов, движущегося в объеме V с абсолютной величиной импульса в интервале {p, p+dp} (в сферических координатах) равно

.                                        (*)

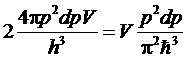В числителе стоит объем в пространстве импульсов и координат, в знаменателе – элементарный объем;

Электроны заполняют все состояния с импульсами от 0 до граничного значения р = рF. Об этом значении говорят как о радиусе ферми-сферы в импульсном пространстве.

Полное число электронов в этих состояниях:

.

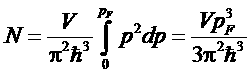Откуда для граничного импульса имеем

.

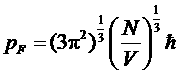И для граничной энергии (для большинства систем энергия рассчитывается по классической формуле, однако есть и исключения – для очень плотных систем энергия должна рассчитывается по релятивистской формуле):

 .

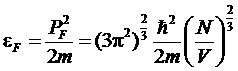Эта энергия называется энергией Ферми. Это энергия имеет простой термодинамический смысл. Функция распределения (число заполнения) Ферми по квантовым состояниям (с определенными значениями импульса p и проекцией спина)

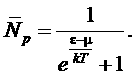
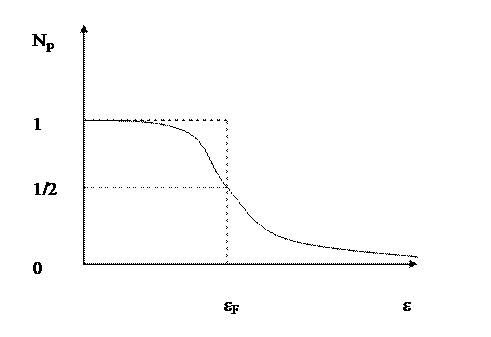
Проанализируем полученное выражение при Т®0. Видно, что при ε < µ это выражение стремится к единице, а при ε > µ стремится к нулю. Тогда можно изобразить график зависимости среднего числа электронов на уровне от энергии электрона:

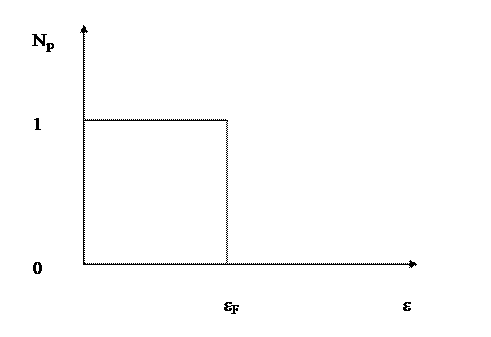
Сравнивая полученную зависимость с распределением электронов при Т = 0, можно видеть, что химический потенциал электронного газа при Т = 0 совпадает с граничной энергией электронов (энергией Ферми): µ = εF. Полная энергия газа получается умножением числа состояний (*) на р2/2m и интегрированием по всем импульсам

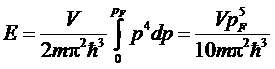
или, подставив выражения для pF, получим

  .                                (**)

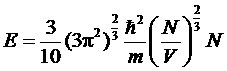Найдем уравнение состояние электронного газа (любого Ферми- газа) при температуре T> 0.

Число частиц в элементе фазового пространства dpxdpydpzdV получится умножением величины

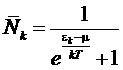   на  ,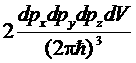

откуда получим

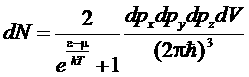
Интегрируя по dV, получим распределение по компонентам импульса частиц, а переходя к сферическим координатам в пространстве импульсов, найдем распределение по абсолютной величине импульса

.

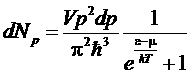Удобно перейти к одной переменной–энергии

.

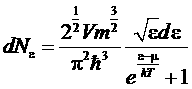Эта формула заменяет классическое распределение Максвелла для случая электронного газа. Интегрируя по de, получим полное число частиц в газе:

.

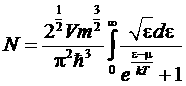Эта формула определяет в неявном виде (поскольку интеграл не берется) химический потенциал газа как функцию от температуры Т и концентрации N/V.

Формулу для большого термодинамического потенциала в случае электронного газа можно представить в виде:

.

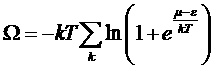Совершая такой же переход от суммирования к интегрированию, который был выполнен при расчете числа электронных состояний, получим выражение для потенциала

.

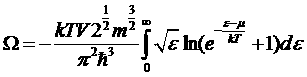Интегрируя по частям, находим

.

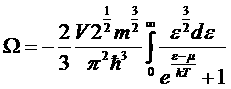Это выражение совпадает с точностью до множителя –2/3 с полной энергией газа

.

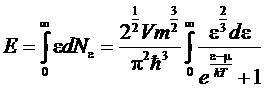Имея также в виду, что:

Ω=F–µN=U–TS + PV–PV–µN = G - µN –PV = –PV,

получим

.

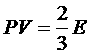Это соотношение должно выполняться и в предельном случае больцмановского газа. Действительно, подставляя больцмановское значение 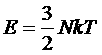, получим , то есть уравнение Менделеева– Клапейрона.

Подставим полученное соотношение в выражение для полной энергии (**), находим уравнение состояния электронного газа (при Т=0К):

.

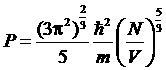Таким образом, давление Ферми-газа при абсолютном нуле температуры пропорционально его концентрации в степени 5/3. Полученная формула применима приближенно также и при температурах, достаточно близких (при данной концентрации газа) к абсолютному нулю. Условие ее применимости (условия «сильного вырождения» газа) требует, очевидно, малости kТ по сравнению с граничной энергией eF:

.

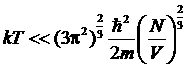Температуру ТF= eF/kназывают температурой вырождения (температурой Ферми). Оказывается, что для большинства металлов эта температура составляет приблизительно 104 К. Отсюда можно сделать вывод, что в металлах электронный газ всегда вырожден.

При температуре, большей 0К график функции распределения Ферми будет иметь следующий вид:

Примером двумерного Ферми-газа является недавно открытый графен.

Рассмотрим теперь теплоемкость Ферми-газа. В случае, когда температура газа много меньше температуры Ферми, все термодинамические величины можно разложить в ряд:

,

,

.

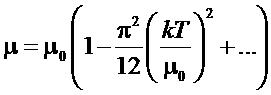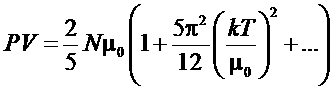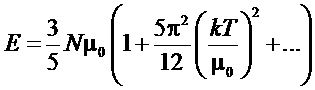Зная энергию, можно вычислить теплоемкость:

.

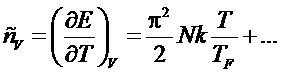Из этого соотношения видно, что теплоемкость электронного газа в металлах при комнатной температуре очень мала по сравнению с теплоемкостью решетки (- закон Дюлонга-Пти).