Сверхплотный ферми-газ и гравитационное равновесие звезд

Эволюция звезд. Белые карлики. Фаулер. Принципиальный интерес представляет исследование свойств вещества при чрезвычайно больших плотностях. Проследим качественно за изменением этих свойств по мере постепенного увеличения плотности.

Когда объем, приходящийся на один атом, становится меньше обычных атомных размеров, атомы теряют свою индивидуальность, так что вещество превращается в сильно сжатую электронно-ядерную плазму. Если температура вещества не слишком высока, то электронная компонента этой плазмы представляет собой вырожденный ферми-газ. Электронный ферми-газ обладает своеобразным свойством: его идеальность возрастает по мере увеличения плотности. Это происходит потому, что кинетическая энергия электронов пропорциональна концентрации в степени 2/3, а кулоновская энергия – лишь 1/3. Поэтому при достаточном сжатии вещества роль взаимодействия электронов с ядрами (и друг с другом) становится несущественной, так что можно пользоваться формулами идеального ферми-газа. Можно показать, что это наступает при выполнении неравенства

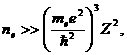
где пе- плотность числа электронов, те - масса электрона, Z-некоторыйсредний атомный номер вещества. Отсюда получаем для полной плотности массы вещества неравенство

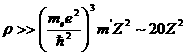 г/см3,                                           

где m’ - масса, приходящаяся на один электрон. Примем, что эта масса равна удвоенной массе нуклона. Что касается «ядерного газа», то благодаря большой массе ядра он еще может быть далек от вырождения, но его вклад, например, в давление вещества совершенно несуществен по сравнению с давлением электронного газа.

Таким образом, термодинамические величины вещества в рассматриваемых условиях определяются формулами, примененными к электронной компоненте. В частности, для давления имеем

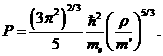
Условие для плотности дает для давления численное неравенство атм.

В написанных формулах электронный газ предполагается нерелятивистским. Это требует малости граничного импульса ФермиρF по сравнению с тс, что приводит к численным неравенствам

Когда плотность и давление газа становятся сравнимыми с указанными значениями, электронный газ делается релятивистским, а при выполнении обратных неравенств - ультрарелятивистским. В последнем случае уравнение состояния вещества определяется формулой

Дальнейшее повышение плотности приводит к состояниям, в которых термодинамически выгодными оказываются ядерные реакции, заключающиеся в захвате электронов ядрами (с одновременным испусканием нейтрино). В результате такой реакции уменьшается заряд ядра.

При еще больших плотностях и давлениях будет происходить дальнейший захват электронов ядрами, сопровождающийся дальнейшим уменьшением заряда последних. Здесь начинается область плотностей, в которой вещество можно рассматривать в основном как вырожденный нейтронный ферми-газ с небольшой примесью электронов и различных ядер, концентрации которых определяются условиями равновесия соответствующих ядерных реакций. Уравнение состояния вещества в этой области есть

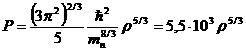атм,                           

где mn– масса нейтрона.

Наконец, при плотностях  г/см3 вырожденный нейтронный газ станет ультрарелятивистским, а уравнение состояния будет определяться формулой

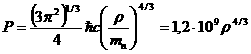атм.                          

Рассмотрим тело очень большой массы, части которого удерживаются вместе силами гравитационного притяжения. Реальные тела большой массы известны нам в виде звезд, непрерывно излучающих энергию и отнюдь не находящихся в состоянии теплового равновесия. Представляет, однако, принципиальный интерес рассмотрение равновесного тела большой массы. При этом мы будем пренебрегать влиянием температуры на уравнение состояния, т.е. будем рассматривать тело находящимся при абсолютном нуле («холодное» тело). Это можно сделать потому, что для сильно вырожденного ферми-газа температуру можно считать равной нулю.

Будем далее предполагать тело невращающимся; тогда в равновесии оно будет иметь сферическую форму, и распределение плотности в нем будет центрально-симметричным.

Равновесное распределение плотности (и других термодинамических величин) в теле будет определяться следующими уравнениями. Ньютоновский гравитационный потенциал φ удовлетворяет дифференциальному уравнению

где ρ – плотность вещества, G– ньютоновская гравитационная постоянная; в центрально-симметричном случае имеем

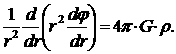
В гравитационном поле потенциальная энергия частицы с массой т'есть т'φ, так что имеем

где т'-масса частицы тела, а у химического потенциала вещества в отсутствие поля для краткости опущен индекс нуль. Выразив φчерез µи подставив в уравнение для потенциала, мы можем написать последнее в виде

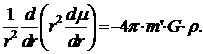
При увеличении массы гравитирующего тела возрастает, естественно, и его средняя плотность (это обстоятельство будет подтверждено следующими ниже вычислениями). Поэтому при достаточно большой полной массе М тела можнорассматривать вещество тела как вырожденный электронный ферми-газ - сначала нерелятивистский, а затем, при еще больших массах, релятивистский.

Химический потенциал (энергия Ферми) нерелятивистского вырожденного электронного газа связан с плотностью тела ρравенством

.                             

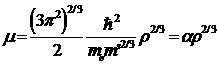Выразив отсюда ρ через µ, получим следующее уравнение:

  (*)

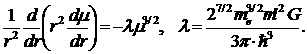Обладающие физическим смыслом решения этого уравнения не должны иметь особенности в начале координат: µ—>const при r —> 0. Это требование автоматически приводит к условию дляпервой производной

  при r = 0.

Ряд существенных результатов можно получить уже путем применения к уравнению (*) простых соображений размерности. Решения уравнения (*) содержат лишь два постоянных параметра - постоянную λ и, например, радиус тела R,заданием которого однозначно определяется выбор решения. Из этих двух величин можно образовать всего одну величину с размерностью длины - самый радиус R,и одну величину с размерностью энергии:  (постоянная λ имеет размерность м-2 • Дж-1/2). Поэтому ясно, что функция µ(r)должна иметь вид

где f- некоторая функция только от безразмерного отношения r/R. Поскольку плотность ρпропорциональна µ3/2, то распределение плотности должно иметь вид

.

Таким образом, при изменении размеров сферы распределение плотности в ней меняется подобным образом, причем в подобных точках плотность меняется обратно пропорционально R6.В частности, средняя плотность сферы будет просто обратно пропорциональна R6:

.

Полная же масса М тела, следовательно, обратно пропорциональна кубу радиуса:

Эти два соотношения можно написать также в виде

Таким образом, размеры равновесной сферы обратно пропорциональны кубическому корню из ее полной массы, а средняя плотность пропорциональна квадрату массы. Последнее обстоятельство подтверждает сделанное выше предположение о том, что плотность гравитирующего тела растет с увеличением его массы.

Тот факт, что гравитирующая сфера из нерелятивистского вырожденного ферми-газа может находиться в равновесии при любом значении полной массы М,можно было усмотреть заранее из следующих качественных соображений. Полная кинетическая энергия частиц такого газа пропорциональна N(N/V)2/3, или, что то же самое, М5/3 / R2, а гравитационная энергия газа в целом отрицательна и пропорциональна M2/R.Сумма двух выражений такого типа может иметь минимум (как функция от R)при любомМ, причем в точке минимума.

.

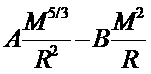Для безразмерной переменной ξ = r/ R получим, что функция  f(ξ) удовлетворяет уравнению

с граничными условиями f ‘(0) = 0; f ‘(1) = 0. Это уравнение не может быть решено в аналитическом виде и должно интегрироваться численно (см, рис). Наконец, для отношения центральной плотности ρ(0) к средней плотности  легко найти

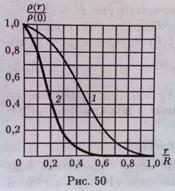
На рисункеизображен график отношения ρ(r)/ρ(0) как функции r/R.

Перейдем к исследованию равновесия сферы, состоящей из вырожденного ультрарелятивистского электронного газа. Полная кинетическая энергия частиц такого газа пропорциональна N(N/V)1/3, или иначе M4/3 / R; гравитационная же энергия пропорциональна -M2/R.Таким образом, обе эти величины зависят от Rодинаковым образом, и их сумма тоже будет иметь вид const•R-1. Отсюда следует, что тело вообще не сможет находиться в равновесии: если const>0,то оно будет стремиться расширяться (до тех пор, пока газ не станет нерелятивистским); если же const<0,то уменьшению полной энергии будет соответствовать стремление Rкнулю, т.е. тело будет неограниченно сжиматься. Лишь вособом случае const=0тело может находиться в равновесии, причем вбезразличном равновесии с произвольными размерами R.

Эти качественные соображения, разумеется, полностью   подтверждаются точным количественным анализом. Химический потенциал рассматриваемого релятивистского газа связан с плотностью соотношением

Вместо уравнения (*) получаем теперь

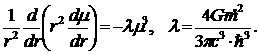
Имея в виду, что λ обладает теперь размерностью Дж-2•м-2, находим, что химический потенциал как функция от rдолжен иметь вид

а распределение плотности

Таким образом, средняя плотность будет теперь обратно пропорциональна R3, а полная масса оказывается не зависящей от размеров постоянной:

M0 есть единственное значение массы, при котором возможно равновесие; при М >М0 тело будет стремиться неограниченно сжиматься, а при М<М0оно будет расширяться.

Для точного вычисления «критической массы» М0 необходимо произвести численное интегрирование уравнения

.

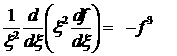Положив m’ = 2mn, получим M0 = 1,45.

На рисунке (кривая 2) дан график ρ(r)/ρ(0) в ультрарелятивистском случае как функции r/R.

Полученные результаты о зависимости междумассойи радиусом равновесного «холодного» сферического тела можно представить во всей области измерения Rв виде единой кривой, определяющей зависимость М = M(R).При больших R(и соответственно малых плотностях тела) электронный газ можно рассматривать как нерелятивистский, и функция M(R)спадает по закону . При достаточно же малых Rплотность настолько велика, что имеет место ультрарелятивистский случай, и функция M(R)имеет почти постоянное (равное М0) значение (строго говоря, M(R) —>M0при R —>0).

Сделанный вывод имеет фундаментальное значение для эволюции звезд. Сейчас ученые уверены, что при достижении звездой определенной массы она превращается в черную дыру. Сверхмассивные черные дыры находятся в центре практически каждой галактики. Полученную оценку критической массы звезды можно рассматривать лишь как приближенную, поскольку точное решение уравнения для гравитационного поля можно получить лишь в рамках общей теории относительности. Кроме того, после первых оценок модели нейтронных звезд были существенно уточнены.

Белые карлики представляют собой компактные звёзды с массами, сравнимыми с массой Солнца, но с радиусами в ~100 км и, соответственно, светимостями в ~10000 раз меньшими солнечной. Плотность белых карликов составляет 108—1012 кг/м³, что почти в миллион раз выше плотности обычных звёзд главной последовательности.

Высокая плотность белых карликов оставалась необъяснимой в рамках классической физики и астрономии и нашла объяснение лишь в рамках квантовой механики после появления статистики Ферми — Дирака. В 1926 году Фаулер в статье «Плотная материя» («On dense matter», Monthly Notices R. Astron. Soc. 87, 114—122) показал, что, в отличие от звёзд главной последовательности, для которых уравнение состояния основывается на модели идеального газа (стандартная модель Эддингтона), для белых карликов плотность и давление вещества определяются свойствами вырожденногоэлектронного газа (ферми-газа).

Следующим этапом в объяснении природы белых карликов стали работы Якова Френкеля и Чандрасекара. В 1928 году Френкель указал, что для белых карликов должен существовать верхний предел массы, и в 1931 году Чандрасекар в работе «Максимальная масса идеального белого карлика» («The maximum mass of ideal white dwarfs», Astroph. J. 74, 81—82) показал, что существует верхний предел масс белых карликов, то есть эти звёзды с массой выше определённого предела неустойчивы (предел Чандрасекара) и должны коллапсировать.

Нейтро́нная звезда́ — астрономический объект, являющийся одним из конечных продуктов эволюции звёзд, состоящий из нейтронной сердцевины и сравнительно тонкой (∼1 км) коры вырожденного вещества, содержащей тяжёлые атомные ядра. Масса нейтронной звезды практически такая же, как и у Солнца, но радиус составляет около 10 км. Поэтому средняя плотность вещества такой звезды в несколько раз превышает плотность атомного ядра (которая для тяжёлых ядер составляет в среднем 2,8·1017 кг/м³). Считается, что нейтронные звезды рождаются во время вспышек сверхновых.Силы тяготения в нейтронных звёздах уравновешиваются давлением вырожденного нейтронного газа.