Вырожденный Бозе-газ. Экспериментальное наблюдение Бозе-Эйнштейновской конденсации

При низких температурах свойства Бозе-газа не имеет ничего общего со свойствами Ферми-газа. Это заранее очевидно из того, что у Бозе-газа состоянием наименьшей энергии, в котором газ находится при
Т = 0, должно быть состояние с Е = 0, в то время, как Ферми-газ при Т=0 обладает отличной от нуля энергией. 

Если при заданной концентрации N/V газа понижать его температуру, то химический потенциал (который можно найти по формуле, аналогичной Ферми)

                                                 (*)

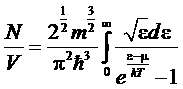будет увеличиваться, т.е. будучи отрицательным, уменьшатся по абсолютной величине.

Он достигает значения μ = 0 при температуре, определяемой соотношением

,

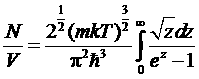где z = ε/kТ – новая переменная.

Входящий сюда интеграл выражается через ξ – функцию Римана (табличный). Обозначая искомую температуру через Т0, получим

  .

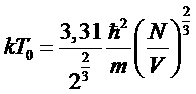       Заметим, что по структуре полученная формула напоминает выражение для энергии Ферми, но поскольку масса бозонов, как правило, значительно больше массы электронов, то температура T0 будет значительно меньше, чем температура Ферми для электронного газа.

При Т<Т0 уравнение (*) не имеет отрицательных решений, между тем как в статистике Бозе химический потенциал должен быть отрицательным при всех температурах (в противном случае число заполнения уровня окажется отрицательным).

Это кажущееся противоречие связано с тем, что в данных условиях не законен переход от суммирования к интегрированию, который выполнялся выше для статистики Ферми.

Действительно, при этом переходе первый член суммы eк = 0 умножается на , то есть выпадает из суммы. Между тем при понижении температуры частицы должны скапливаться именно в этом состоянии с наименьшей энергией, пока при Т = 0 туда не попадут все они.

Математически это обстоятельство проявляется в том, что в сумме

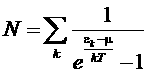
при переходе к пределу µ®0 сумма всех членов ряда, за исключением первого стремится к конечному пределу, определяемому интегралом

,

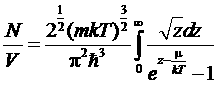а первый член с εк = 0 стремится к бесконечности. Устремляя µ не к нулю, а к некоторому малому конечному значению, можно, следовательно, предать указанному первому члену суммы требуемое конечное значение.

Поэтому в действительности при Т<T0 дело будет обстоять следующим образом. Частицы с энергией ε > 0 будут распределены по функции:

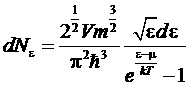
с µ = 0

.

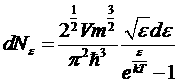Полное число частиц с энергиями ε> 0 будет, следовательно, равно

.

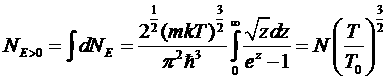Остальные

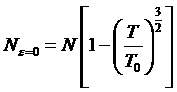
частицы находятся в низшем состоянии, т.е. имеют энергию e=0. Это явление называют конденсацией Бозе-Эйнштейна. Название происходит от аналогии с конденсацией газа в жидкость, однако здесь имеется в виду конденсация в импульсном пространстве.

Заметим, что само это явление было предсказано Эйнштейном, на основе полученного им ранее распределения для произвольных частиц с целым спином.

Энергия газа при Т < Т0 определяется, конечно только теми частицами, которые имеют энергию больше ноля.

Полагая в

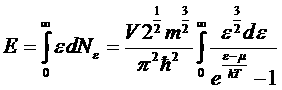
µ=0, имеем

.

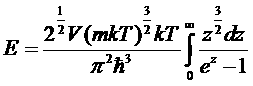Этот интеграл приводится к табличному, тогда получим

.

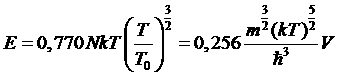Отсюда теплоемкость

,

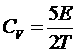То есть теплоемкость пропорциональна Т3/2. Интегрируя теплоемкость, находим энтропию

,

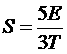и свободную энергию F = E–TS = –2/3 E

Последний результат вполне естественен, так как при µ=0
F= Nµ+Ω=Ω. Для давления P=–(∂F/∂V)Tимеем

.

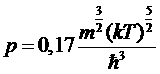Мы видим, что при Т<Т0 давление пропорционально Т5/2 и не зависит вовсе от объема. Это обстоятельство – естественно следствие того, что частицы, находящиеся в состоянии с e=0, не обладая импульсом, не дают никакого вклада в давление. В самой точке Т = Т0 все перечисленные термодинамические величины непрерывны. Можно, однако, что производная от теплоемкости по температуре испытывает в этой точке скачок.

Аналогия с давлением в двухфазной системе для газа Ван-дер-Ваальса.

Удельная теплоемкость идеального Бозе-газа.

В каких системах можно наблюдать явление Бозе-конденсации? Во-первых, это должны быть бозоны с неравным нулю химическим потенциалом. Как будет показано ниже, фотоны, являясь бозонами, имеют химический потенциал, равный нулю. Поэтому для излучения такой эффект не имеет места. С другой стороны, это должна быть идеальная система, в которой взаимодействие между частицами мало (все полученные нами формулы выведены именно в этом предположении). Последнее означает, что переход к сверхтекучему состоянию в жидком гелии, происходящий при T» 2,2 К не может быть интерпретирован как конденсация Бозе-Эйнштейна, поскольку в жидкости взаимодействие между атомами велико. И хотя связь между Бозе-конденсацией и переходом гелия в сверхтекучее состояние существует, этот случай требует отдельного рассмотрения.

Экспериментальное наблюдение Бозе-Эйнштейновской конденсации

Шведская Королевская академия наук присудила Нобелевскую премию 2001 г. по физике работающим в США ученым Э.Корнеллу, В.Кеттерле и К.Вайману “за экспериментальное обнаружение конденсации Бозе-Эйнштейна в разреженных газах щелочных металлов и фундаментальные исследования свойств конденсата”.

С тех пор как Альберт Эйнштейн в предсказал новое интересное явление, история его изучения была очень непростой. В 1924 г. Эйнштейн сделал первый весьма неординарный шаг: перенес статистику, предложенную индийским физиком Шатьендранатом Бозе для фотонов, на материальные частицы. В следующем году, анализируя поведение системы таких частиц, Эйнштейн обнаружил, что в ней возможно явление, которое сейчас получило название конденсации Бозе-Эйнштейна.

Утверждение Эйнштейна нетривиально по двум причинам. Во-первых, рассматривается газ невзаимодействующих частиц. Во-вторых, речь идет о конечной температуре, и в этом случае естественно думать, что все частицы “размазаны” по разным энергетическим состояниям. Не случайно после опубликования данной работы очень крупные физики-теоретики высказывали сомнения в ее достоверности. Достаточно вспомнить Дж.Уленбека, который считал этот результат артефактом, или П.Эренфеста, близкого друга Эйнштейна, который писал в своем письме последнему, что предсказанное им явление неявно предполагает наличие взаимодействия между частицами. В ответном письме Эйнштейн признавал, что это, по-видимому, так, и он затрудняется это интерпретировать, но не сомневается: конденсация - прямой результат статистических свойств газа независимых частиц.

Чтобы понять, почему возникали такие сомнения, надо упомянуть ряд обстоятельств. К тому моменту еще не существовало двух статистик, которые мы теперь знаем под именами Бозе-Эйнштейна и Ферми-Дирака, т.е. не было раздельного описания для частиц с целочисленным спином (первая статистика) и полуцелым спином (вторая). Не было и осознания решающего факта, что в квантовой механике волновая функция, соответствующая двум или более идентичным частицам, при перестановке их местами не должна меняться (статистика Бозе-Эйнштейна) или, наоборот, должна менять знак (статистика Ферми-Дирака). Именно эта обязательная симметризация - исключительно нетривиальное обстоятельство - фактически вводит некое виртуальное взаимодействие между частицами в случае, когда непосредственного, силового взаимодействия между ними нет. Бозе-эйнштейновская конденсация часто называется просто бозе-конденсацией, хотя в работе Бозе о конденсации нет ни единого слова (он рассматривал газ равновесных фотонов, где это явление отсутствует).

Однако прямого экспериментального наблюдения непосредственно самой конденсации до 1995 г. не было. Это обстоятельство не случайно: чтобы ее наблюдать, необходимо иметь газ при фантастически низких температурах. В первых экспериментах температура была в 10 млрд раз ниже комнатной, а ведь даже при температуре около 1 К любые вещества становятся твердыми (единственное исключение - гелий, остающийся жидким). Рассчитывать, что при такой температуре может существовать газ, просто невероятно. Поэтому речь могла идти только о метастабильном состоянии, т.е. о том, чтобы искусственно приготовить газ, который “жил” бы достаточное для эксперимента время. Но тут же возникает и вторая проблема: этот газ не должен взаимодействовать со стенками сосуда, который его удерживает, поскольку при таких температурах любое взаимодействие со стенками разрушит метастабильное состояние.

Итак, необходимо иметь, с одной стороны, рекордно низкие температуры, а с другой - систему, в которой газ не имеет контакта со стенками. Последнее препятствие было преодолено таким образом: роль сосуда играло магнитное поле определенной конфигурации. В так называемой магнитной ловушке частицы с магнитным моментом при достаточно низкой температуре испытывают фактически только отражение от магнитной “стенки”, т.е. никакого реального физического контакта нет, и газ существует в системе с абсолютно отражающими стенками. Получить же столь низкие температуры (это была фундаментальная проблема) удается лишь в два этапа. На первом используется метод лазерного охлаждения. Если поток фотонов падает на взаимодействующие с ним атомы и рассеивается, то импульс фотонов передается последним. При этом частицы, двигающиеся навстречу фотонам, получают импульс в противоположном направлении, т.е. происходит их замедление. Заставить взаимодействовать с фотонами нужную группу атомов можно, подбирая соответствующим образом частоту лазера - так, чтобы она резонансно совпала с частотой поглощения фотона атомом, зависящей из-за эффекта Доплера от его движения. Работы по лазерному охлаждению получили Нобелевскую премию в 1997 году (С.Чу, К.Коэн-Таннуджи, У.Д.Филлипс), и столь высокая оценка, была обусловлена именно тем, что оно было использовано при охлаждении газов для достижения бозе-конденсации. Таким образом, удается эффективно охладить до 10–4-10–5К довольно большое число атомов, однако эти температуры все еще недостаточны для поставленной цели.

Чтобы до конца охладить систему, нужен второй этап, и им стало так называемое испарительное охлаждение. Если внутри какого-нибудь сосуда с барьерами находятся атомы, то наиболее горячие атомы или, как говорят, максвелловские хвосты распределения преодолевают барьер, а те, которые имеют более низкую энергию, через барьер выйти не могут. Поэтому со временем, за счет “обрезания” этих “хвостов”, происходит понижение температуры в системе. Если уменьшить высоту барьера, через него уйдут и другие частицы, обладающие уже меньшей энергией. Так, постепенно понижая барьер, можно достичь исключительно низких температур, сохраняя при этом достаточно большое количество частиц в системе.

Этот метод был развит еще до исследований лауреатов, но они усовершенствовали его, используя для “обрезания хвостов” парамагнитный резонанс. Поскольку в данном случае частицы удерживаются в магнитной ловушке, можно, подавая переменное поле, “приоткрывать” ловушку тем из них, для которых выполнено условие парамагнитного резонанса, вызывая их ускоренный уход. Снижая по мере отсева горячих атомов частоту электромагнитного поля, можно постепенно “срезать” слои теплых частиц. Сочетание лазерного охлаждения и ускоренного испарения позволило достичь температуры в 10–8К, и к 1995 г. в двух лабораториях был получен газ, который, с одной стороны, имел такую низкую температуру, а с другой - достаточно большое количество частиц. В лаборатории JILA, объединенного исследовательского центра Национального института стандартов и Колорадского университета, охлаждение было выполнено для 2000 атомов рубидия, а в Массачусетсском технологическом институте - для еще большего числа (порядка 105) атомов натрия.

Почему были выбраны именно натрий и рубидий? По двум причинам. Во-первых, они представляют собой простейшую систему: щелочные металлы, как и атомарный водород, имеют один электрон на внешней оболочке и, следовательно, имеют спин и магнитный момент (все удержание происходит в магнитных ловушках, которые “держат” незаряженные частицы за счет взаимодействия атома, обладающего магнитным моментом, с магнитным полем). Необходимое качество присутствует у всех трех упомянутых элементов. Во-вторых, щелочные элементы имеют подходящие частоты переходов, соответствующие сравнительно стандартным лазерам.